Exemple
Le potentiel du marché est fixé à 1000, la durée du processus analysé est de 20 périodes le facteur externe (effet de publicité) a=0,01 et le facteur interne (importance du bouche à oreille) b=0,001. [2.65]
Listing 22
1. a=0.01 # external factor
2. b=0.001 # internal factor
3. ycum=0
4. y<-rep(0,20)
5. for(i in 2:20){
6. y[i]<-(a+b*y[i-1])*(1000-ycum)
7. ycum=ycum+y[i]
8. }
9. y
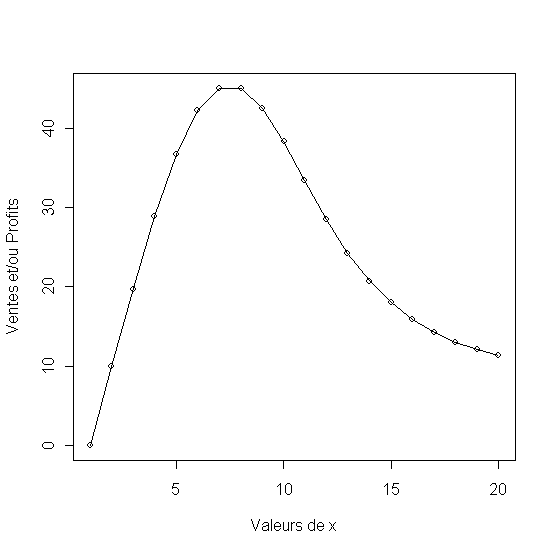
10. matplot(1:20, y, pch = 1:1, type = "o", col = 1:1,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
Analyse
Les premières quatre lignes de code donnent des valeurs aux variables a, b et initialisent la variable ycum et le vecteur y à zéro.
Les lignes 5 et 8 renferment une boucle ou i progresse de 2 à 20. Pour chaque i à la ligne 6 la ième valeur du vecteur y est le produit de 1000 moins ycum et d'une fonction linéaire de sa valeur précédente y[i-1]. ycum est la somme cumulée durant i étapes du vecteur y. La ligne 9 affiche les valeurs du vecteur y à la fin du processus (boucle) et la ligne dix représente graphiquement les valeurs de y qui correspondent à chaque période.
La relation dans la boucle veut dire que y[i] le nombre d'adopteurs du nouveau produit à la période i dépend du nombre de nombre de clients potentiels n'ayant pas encore adopté le produit (1000-ycum) pondéré par un facteur externe comme l'effet de la publicité (a) et un effet de bouche à oreille qui lui dépend des nouveaux adopteurs de la période précédente y[i-1] multiplié par le facteur interne (b).
Figure 29 - Les cycle e vie d'un produit exprimé en terme de ventes (modèle de diffusion de Bass)