Exemples
On utilise les modèle d'efficacité des dépenses publicitaires 2.30 et 2.31 (publicité statique optimum est 10 et prix statique optimal = 6
- Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,2) dépense constante[2.59.1]
- Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,2) dépenses par impulsions [2.59.2]
- Effets dynamiques des dépenses publicitaires, fort effet dynamique (0,8) dépense constante[2.59.3]
- Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,8) dépenses par impulsions [2.59.4]
- Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,8) dépense constante sous contrainte budgetaire[2.59.5]
- Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,8) dépenses par impulsions sous contrainte budgetaire[2.59.6]
Listing 21
1. x2=rep(6,10)
2. x1=rep(15,10)
3. alfa=0.8
4. lambda=0.2
5. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2
6. y<-rep(0,10)
7. y[1]<-ylong[1]
8. for(i in 2:10){
9. y[i]<-alfa*ylong[i]+lambda*y[i-1]
10. }
11. profit<-(x2-1.5)*y-x1
12. df<-data.frame(Ventes=y, Profit1=profit)
13. x1=rep(c(25,5),5)
14. alfa=0.8
15. lambda=0.2
16. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2
17. y<-rep(0,10)
18. y[1]<-ylong[1]
19. for(i in 2:10){
20. y[i]<-alfa*ylong[i]+lambda*y[i-1]
21. }
22. profit<-(x2-1.5)*y-x1
23. df$Profit2=profit
24. x1=rep(15,10)
25. alfa=0.2
26. lambda=0.8
27. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2
28. y<-rep(0,10)
29. y[1]<-ylong[1]
30. for(i in 2:10){
31. y[i]<-alfa*ylong[i]+lambda*y[i-1]
32. }
33. profit<-(x2-1.5)*y-x1
34. df$Profit3=profit
35. x1=rep(c(25,5),5)
36. alfa=0.2
37. lambda=0.8
38. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2
39. y<-rep(0,10)
40. y[1]<-ylong[1]
41. for(i in 2:10){
42. y[i]<-alfa*ylong[i]+lambda*y[i-1]
43. }
44. profit<-(x2-1.5)*y-x1
45. df$Profit4=profit
46. x1=rep(5,10)
47. alfa=0.2
48. lambda=0.8
49. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2
50. y<-rep(0,10)
51. y[1]<-ylong[1]
52. for(i in 2:10){
53. y[i]<-alfa*ylong[i]+lambda*y[i-1]
54. }
55. profit<-(x2-1.5)*y-x1
56. df$Profit5=profit
57. x1=rep(c(9,1),5)
58. alfa=0.2
59. lambda=0.8
60. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2
61. y<-rep(0,10)
62. y[1]<-ylong[1]
63. for(i in 2:10){
64. y[i]<-alfa*ylong[i]+lambda*y[i-1]
65. }
66. profit<-(x2-1.5)*y-x1
67. df$Profit6=profit
68. df
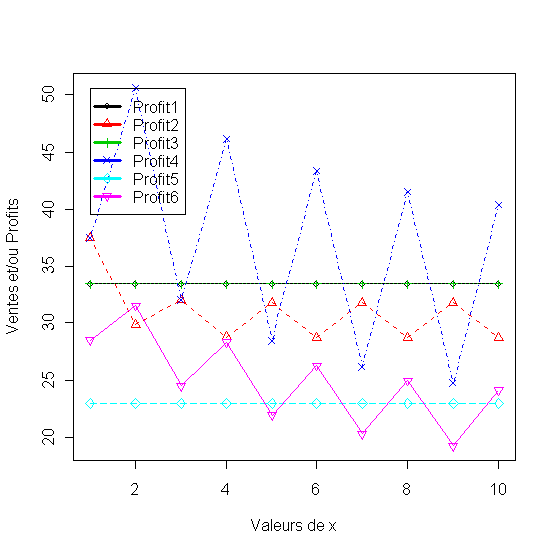
69. matplot(1:10, df[,2:7], pch = 1:6, type = "o", col = 1:6,xlab="Valeurs de x", ylab="Ventes et/ou Profits"
70. legend(1, max(df[,2:7]),names(df)[2:7], lwd=3, col=1:6, pch=1:6)
Figure 28 - Depenses publicitaires constantes ou par impulsion et effets dynamiques