Modèles multiplicatifs
modèle Log-Linéaire
Q = ao![]()
on peut montrer que a1, a2 .. an sont des coefficients d'élasticité
Exemples :
- Modèle loglinéaire recherche du prix optimum en gardant la pub. Fixé à 2 [ 2.30]
- Modèle loglinéaire recherche du prix optimum en gardant la pub. Fixé à 8 [ 2.30_2]
Listing 16
1. x1<-rep(2,10)
2. x2<-seq(3,12,1)
3. y<-100*((+1*x1))^0.5*((+1*x2))^-2
4. profit<-(x2-3)*y-x1
5. df<-data.frame(Effort=x2, Profit2=profit)
6. x1<-rep(8,10)
7. y<-100*((+1*x1))^0.5*((+1*x2))^-2
8. profit<-(x2-3)*y-x1
9. df$Profit8=profit
10. df
11. matplot(x2, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
12. legend(min(x2), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)
Analyse:
En utilisant un modèle de réponse loglinéaire on cherche le prix (x2) optimum en fixant le budget de publicité (x1) dans un première étape à 2 et on calcul le profit (Profit2), ensuite on fait le même calcul avec le budget de pub. fixé à 8 pour obtenir une autre courbe du profit (Profit8).
Figure 19 - Le profit par rapport aux prix et deux niveaux de budget de publicité

Le prix optimum est proche de 6.
- Modèle loglinéaire recherche du niveau de pub optimum avec le prix fixé à son optimum [ 2.30_3]
- Modèle loglinéaire recherche du niveau de pub optimum avec le prix fixé au double de son optimum [ 2.30_4]
Listing 17
1. x1<-seq(0,45,1)
2. x2<-rep(6,46)
3. y<-100*((+1*x1))^0.5*((+1*x2))^-2
4. profit<-(x2-3)*y-x1
5. df<-data.frame(Effort=x1, Profit6=profit)
6. x2<-rep(12,46)
7. y<-100*((+1*x1))^0.5*((+1*x2))^-2
8. profit<-(x2-3)*y-x1
9. df$Profit12=profit
10. df
11. matplot(x1, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
12. legend(min(x1), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)
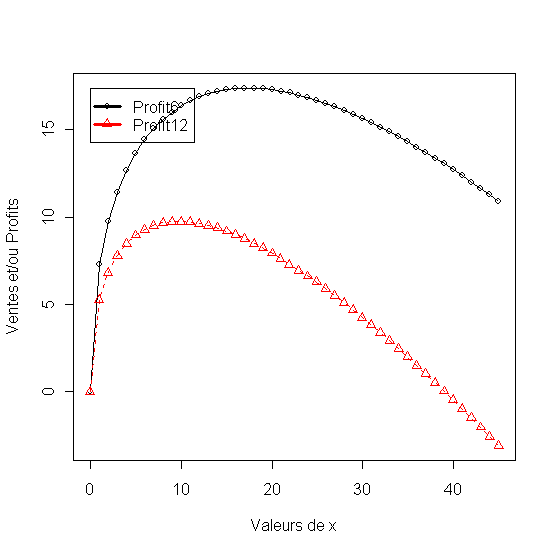
Analyse:
En posant le prix a sont niveau optimum determiné précédament (x2=6) on fait varier le budget du publicité pour obtenir une première courbe du profit (Profit6). Ensuite on double le prix (x2=12) et on applique la même variation de la publicité. Resulte une deuxième courbe du profit (Profit12)
Figure 20 - Le profit par rapport aux dépenses publicitaires et deux niveaux de prix