Adjonction d'interaction
Q = ao + a1 g1 (X1) + a2 g2 (X2) + a3 g1 (X1) g2 (X2)
Exemples :
- Modèle à deux variables avec interaction positive [ 2.24]
- Modèle à deux variables avec interaction negative [ 2.25]
Listing 15
1. a=10
2. b=0
3. c=2
4. d1=2
5. d2=1.5
6. x1<-seq(0,9,1) # publicite varie
7. x2<-rep(5,10) # force de vent fixé a 5
8. g1<-b+(a-b)*((x1)^c/(d1^c+(x1)^c))
9. g2<-b+(a-b)*((x2)^c/(d2^c+(x2)^c))
10. y<-15+1*g1+1.6*g2
11. df<-data.frame(Effort=x1, Ventes.Interaction0 = y)
12. y<-15+1*g1+1.6*g2+0.05*g1*g2
13. df$Ventes.Interact.Pos = y
14. y<-15+1*g1+1.6*g2-0.05*g1*g2
15. df$Ventes.Interact.Neg = y
16. df
17. matplot(x1, df[,2:4], pch=1:4, type = "o", col = 1:3, xlab="Valeurs de x", ylab="Ventes et/ou Profits"
18. legend(min(x), max(df[,2:4]),names(df)[2:4], lwd=3, col=1:3, pch=1:3)
Analyse:
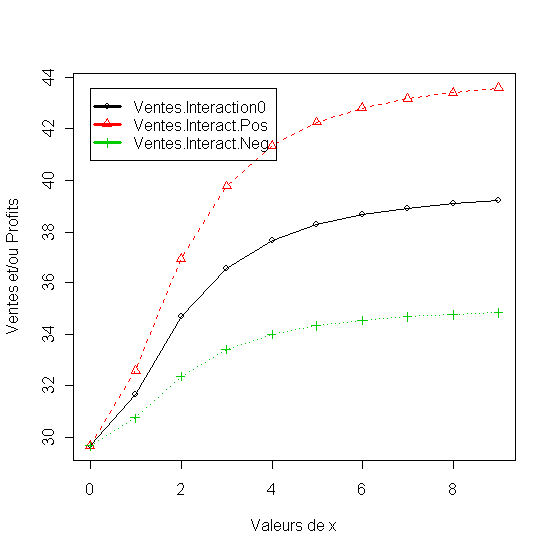
Pour illustrer les effets d'interaction entre les variables du mix marketing le modèle précedent est repris en utilisant un budget de publicité qui varie et un taille de la force de vente fixé à 5. Trois cas de figure sont présentés: le premièr sans interaction entre les deux variables, le deuxième avec un interaction positive et le dernier avec un interaction negative
Figure 18 - Effet d'interaction zero, positive et negative entre deux variable du mix marketing