Modèles Nonlinéaires
Q = ao + a1 g1 (X1) + a2 g2 (X2) + .. + ak gk (Xk)
Exemples :
- Modele Adbudg, lègèrement plus sensible à la publicité qu'à la force de vente [ 2.21]
- Modele Adbudg, lègèrement moins sensible à la force de vente qu'à la publicité[ 2.21_2]
Listing 13
1. a=10
2. b=0
3. c=2
4. d=2
5. x<-seq(0,10,1)
6. y<-b+(a-b)*((x)^c/(d^c+(x)^c))
7. df<-data.frame(Effort=x, Ventes.ForceV=y)
8. d=1.5
9. y<-b+(a-b)*((x)^c/(d^c+(x)^c))
10. df$Ventes.Pub=y
11. df
12. matplot(x, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits"
13. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)
Analyse:
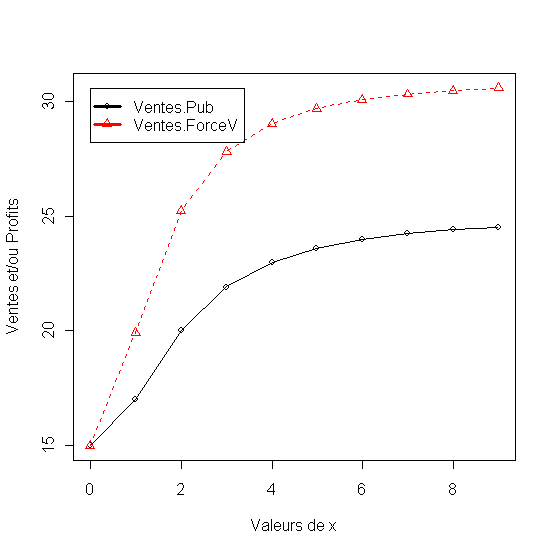
On utilise le modèle Adbudg lègèrement plus sensible grace au coefficient d=2 pour representer la réponse (Ventes.Pub) aux budget de publicité, et un modèle lègèrement moins sensible d=1.5 pour représenter la réaction (Ventes.ForceV) à taille de la force de ventes.
Figure 16 - Modèles Adbudg pour representer la sensibilité des ventes à la publicité et à la force de ventes.

- Modèle à deux variables sans interactions [ 2.23]
Listing 14
1. a=10
2. b=0
3. c=2
4. d1=2
5. d2=1.5
6. x1<-seq(0,9,1) # varie
7. x2<-rep(0,10) # fix
8. g1<-b+(a-b)*((x1)^c/(d1^c+(x1)^c))
9. g2<-b+(a-b)*((x2)^c/(d2^c+(x2)^c))
10. y<-15+1*g1+1.6*g2
11. df<-data.frame(Effort=x1, Ventes.Pub=y)
12. x1<-rep(0,10) # fix
13. x2<-seq(0,9,1) # varie
14. g1<-b+(a-b)*((x1)^c/(d1^c+(x1)^c))
15. g2<-b+(a-b)*((x2)^c/(d2^c+(x2)^c))
16. y<-15+1*g1+1.6*g2
17. df$Ventes.ForceV=y
18. df
19. matplot(x2, df[,2:3], pch=1:2, type = "o", col = 1:2, xlab="Valeurs de x", ylab="Ventes et/ou Profits")
20. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)
Analyse:
Malgrè le faite que le marché est légèrement plus sensible à la publicité, la force de vente est plus efficace avec un poids de 1.6 par rapport a seulment 1 pour la publicité dans le modèle qui regroupe les deux variables. Pour mettre en valeur cette différence d'efficacité on calcule deux cas de figure extrèmes. La premiere represente la réponse (Ventes.Pub) quand la taille de la force de ventes est réduite à zero et la publicité varie. La deuxieme represente la réponse (Vente.ForceV) quand la publicité est réduite à zéro et la taille de la force de vente varie.
Figure 17 - Modèle