Exemples :
- Modele Gompertz, approche lentement la saturation [ 2.19]
- Modele Gompertz, approche la saturation à une vitesse moyenne [ 2.19_2]
- Modele Gompertz, approche rapidement la saturation [ 2.19_3]
- Modele Gompertz, modification de l'origine [ 2.19_4]
Listing 11
1. a=10
2. b=0.1
3. c=0.2
4. d=0
5. x<-seq(0,10,1)
6. y<-a*b^c^(x)+d
7. df<-data.frame(Effort=x, Ventes=y)
8. c=0.6
9. y<-a*b^c^(x)+d
10. df$Ventes2<-y
11. c=0.9
12. y<-a*b^c^(x)+d
13. df$Ventes3<-y
14. b=0.2
15. c=0.6
16. y<-a*b^c^(x)+d
17. df$Ventes4<-y
18. df
19. matplot(x, df[,2:5], pch = 1:4, type = "o", col = 1:4,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
20. legend(min(x), max(df[,2:5]),names(df)[2:5], lwd=3, col=1:4, pch=1:4)
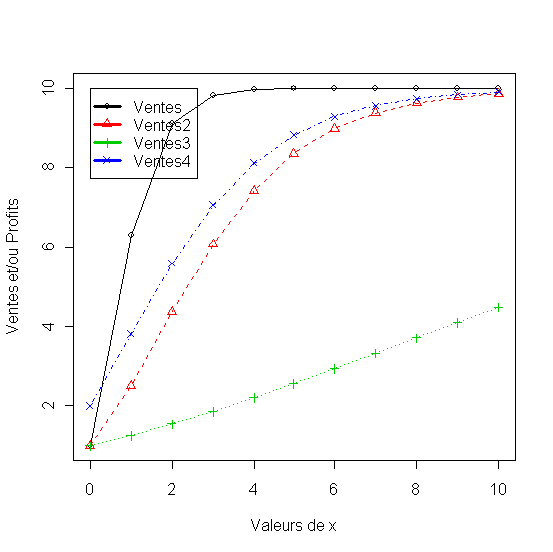
Analyse:
Les premieres trois formulations du modele Gompertz jouent sur l'augmentation du coefficient c. Quand c=0.2, la réponse (Ventes) approche rapidement la saturation. Quand c=0.6 elle approche la saturation à une vitesse moyenne (Ventes2) et quand c=0.9 elle approche lentement la saturation (Ventes3). La modification du coefficient b augmente le niveau de l'origine de la réponse (Ventes4)
Figure 14 - Modèle Gompertz