Modèles Semi-logarithmique
Q = ao + a1 ln(X)
Forme : concave
Réponse marginale : b ea0/a1 quand x = e-a0/a1
Limite inf. (X-->0) : 0 quand x = e-a0/a1
Limite sup. (X-->0) : illimité
Listing 7
1. a=1
2. b=1
3. x<-seq(1,10,1)
4. y<-a+b*log(x)
5. df=data.frame(Effort=x, Ventes=y)
6. a=0
7. y<-a+b*log(x)
8. df$Ventes2=y
9. b=2
10. y<-a+b*log(x)
11. df$Ventes3=y
12. matplot(x, df[,2:4], pch = 1:3, type = "o", col = 1:3,xlab="Valeurs de x", ylab="Ventes et/ou Profits"
13. legend(min(x), max(df[,2:4]),names(df)[2:4], lwd=3, col=1:3, pch=1:3)
Analyse:
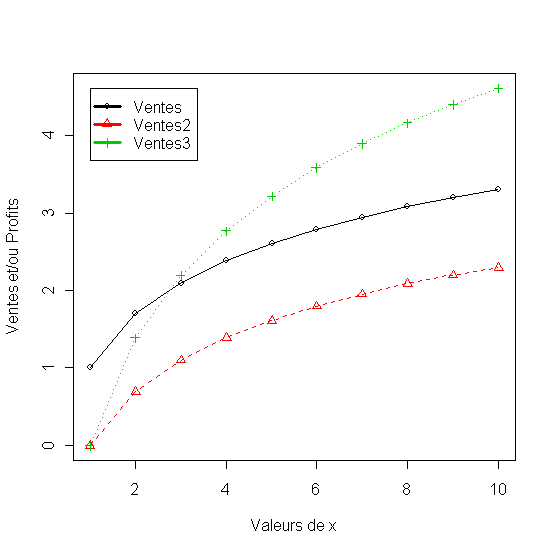
Vue les contrainte imposés par la définition des logarithme ici la valeur minimum de x est 1. La premiere formulation de la réaction de ventes pose a=1 qui indique la valeur minimum de la fonction. Dans les autre deux formulations a=0 d'abord avec b=1 pour donner un deuxième courbe (Ventes2) et ensuite b=2 ce qui imprime au ventes une croissance plus importante (Ventes3).
Figure 10 - Modèle semilogarithmique