Exemples :
- Modèle de Racine Fractionnelle, rythme décroissant applicable aux prix [ 2.15]
- Modèle de Racine Fractionnelle, accroissement à rythme décroissant [ 2.15_2]
Listing 4
1. a=0
2. b=1
3. c=-0.5
4. d=0
5. x<-seq(1,10,1)
6. y<-a+b*(x)^c
7. profit<-0.3*y-x
8. df<-data.frame(Effort=x, Ventes=y, Profit=profit)
9. c=0.5
10. y<-a+b*(x)^c
11. profit<-0.3*y-x
12. df$Ventes2=y
13. df$Profit2=profit
14. df
15. # show Ventes
16. matplot(x, df[,seq(2,5,2)], pch = 1:2, type = "o", col = 1:2,xlab="Effort", ylab="Reponse")
17. legend(min(x), max(df[,seq(2,5,2)]),names(df)[seq(2,5,2)], lwd=3, col=1:2, pch=1:2)
Analyse:
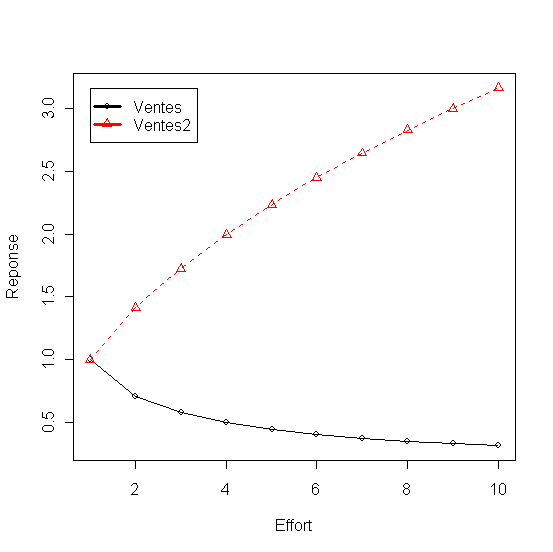
On calcule d'abord un modèle à racine fractionnelle avec un rythme décroissant indique par le coeffcient c (c=-0.5) . Il est applicable aux prix. Quand le coefficient c est positif mais infériur a 1 (ici c= 0.5) on enregistre un acroissement des ventes à rythme décroissant (Ventes2).
Figure 7 - Réponse à rythme décroissant et réponse avec accroissement à rythme décroissant
- Modèle de Racine Fractionnelle, rythme croissant [ 2.15_3]
Listing 5
1. a=0
2. b=1
3. c=1.5
4. d=0
5. x<-seq(1,10,1)
6. y<-a+b*(x)^c
7. matplot(x, y, pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
Analyse:
Quand le coefficient c est positif et supérieur à 1 (ici c=1.5) on obtient une réponse à rythme croissant.
Figure 8 - Modèle de réponse à rythme croissant
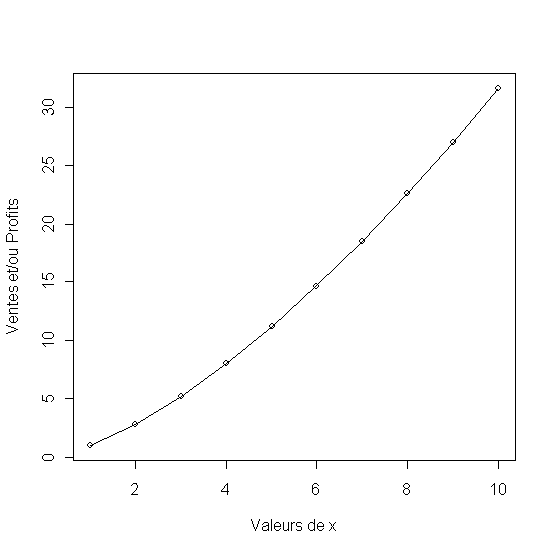
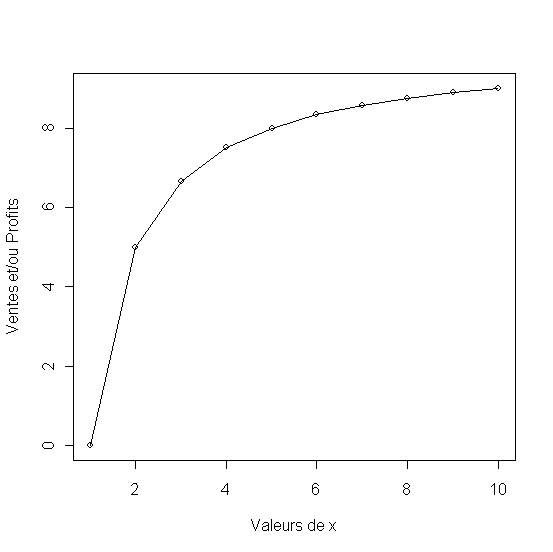
- Modèle de Racine Fractionnelle, equivalent au modèle de saturation [2.15_4]
Listing 6
1. a=10
2. b=-10
3. c=-1
4. x<-seq(1,10,1)
5. y<-a+b*(x)^c
6. matplot(x, y, pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
Analyse
Une forme particulière de réponse obtenue du même modèle de racine fractionnelle, est le modèle de saturation. Dans ce cas le coefficient c=-1. Le modèle devient alors y=a+b/x ou a exprime le niveau de saturation (ici a=10) et b est negatif. Ici b=-a pour que la réponse soit égale à zero quand x = 1.
Figure 9 - Modèle de saturation