Exemples
- Modèle Adbudg initial pour 2Mil. pub 45 Mil. Ventes [ 2.1]
- Modèle Adbudg avec inflexion pour 2Mil. pub 55 Mil. Ventes [ 2.2]
- Modèle Adbudg accéléré pour 1 Mil. pub 45 Mil. Ventes [2.3]
Listing 1
1.
a=60
2.
b=30
3.
c=1
4.
d=2
5.
x<-seq(0,5,1)
6.
y<-b+(a-b)*((x)^c/(d^c+(x)^c))
7.
profit<-0.3*y-x
8.
df<-data.frame(Effort=x, Ventes=y, Profit=profit)
9.
c=2
10.
d=3.32
11.
y<-b+(a-b)*((x)^c/(d^c+(x)^c))
12.
profit<-0.3*y-x
13.
df$Ventes2=y
14.
df$Profit2=profit
15.
c=1
16.
d=1
17.
y<-b+(a-b)*((x)^c/(d^c+(x)^c))
18.
profit<-0.3*y-x
19.
df$Ventes3=y
20.
df$Profit3=profit
21.
# show Ventes
22.
matplot(x, df[,seq(2,7,2)], pch = 1:3, type = "o", col =
1:3,xlab="Effort", ylab="Reponse"
23.
legend(min(x), max(y),names(df)[seq(2,7,2)], lwd=3, col=1:3,
pch=1:3)
24.
# show Profits
25.
matplot(x, df[,seq(3,7,2)], pch = 1:3, type = "o", col = 1:3,xlab="Effort",
ylab="Reponse")
26.
legend(min(x), max(profit),names(df)[seq(3,7,2)], lwd=3, col=1:3,
pch=1:3)
Analyse:
En fixant les coefficients initiaux du modèle a=60, b=30, c=1 et d=2 on calcule les ventes et le profit qui varie entre 0 et 5. En augmentant le coefficient d (d=3.32) on diminue la réactivité du modèle qui se reflètent dans le ventes et dans le profit (Ventes2 et Profit2). Le coefficient c augmenté à 2 a pour éffet d'accroître la valeur du dénominateur par rapport au numérateur quand les x sont petits et de l'inverser ensuite ce qui génre une inflexion et donne au modèle l'allure d'une vraie courbe en "S". En diminuant le coefficient d (d=1) la réactivité du modèle devient supérieure au modèle initiale (Ventes3 et Profit3) et en remettant c=1 le modèle perd sa forme en "S".
Tableau 2 - Ventes et Profit obtenu en faisant varier les coeficients du modèle de réponse (ADBUDG)
Effort Ventes Profit Ventes2 Profit2 Ventes3 Profit3
1 0 30.00000 9.00000 30.00000 9.000000 30.0 9.00
2 1 40.00000 11.00000 36.94444 10.083333 45.0 12.50
3 2 45.00000 11.50000 41.27820 10.383459 50.0 13.00
4 3 48.00000 11.40000 44.24051 10.272152 52.5 12.75
5 4 50.00000 11.00000 46.39344 9.918033 54.0 12.20
6 5 51.42857 10.42857 48.02885 9.408654 55.0 11.50
Figure 1 - Ventes obtenues en faisant varier les coeficients du modèle de réponse à la publicité (ADBUDG)

Figure 2 - Profit enregistré en faisant varier les coeficients du modèle de réponse à la publicité (ADBUDG)
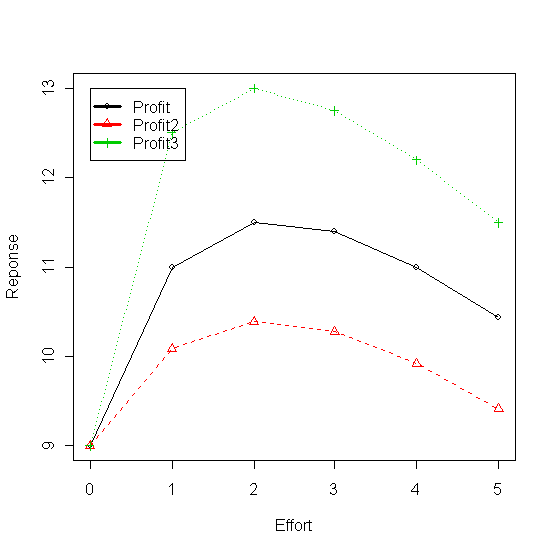
Le graphique montre que la dépense publicitaire optimum avoisine 2 milions de euros.
Critères de classification des modèles de réponse









