L'interaction du mix
Exemples
- Modèle ou l`élasticité prix est fonction de l`effort publicitaire [ 5.1-3]
En simplifiant l'état des connaissance actuel en la matière on peut dire qu'un publicité déstiné à différencier néttement un produit peut faire baisser l'élasticité aux prix, et qu'un publicité destiné à méttre en valeur le rapport qualité/prix peut accroître cette elasticité.
Listing 35
1. # Modèle ou l`elasticité prix est fonction de l`effort publicitaire
2. x1<-seq(0,5,0.5)
3. x2<-rep(11,11)
4. f1 <- 0.2+2.3*x1^1.5/(3.5^1.5+x1^1.5) # pub 5.2
5. f2 <- 5*x2^(-0.25*(x1-4)) # prix 5.3
6. y<-100*f1*f2 # 5.1
7. profit<-(x2-3)*y-x1
8. df<-data.frame(Pub=x1, Ventes=y, Profit=profit)
9. f2 <- 5*x2^(-0.25*(1.5-4)) # elasticité du prix fixe pour une pub de 1.5
10. y<-100*f1*f2 # 5.1
11. profit<-(x2-3)*y-x1
12. df$Profit2=profit
13. df
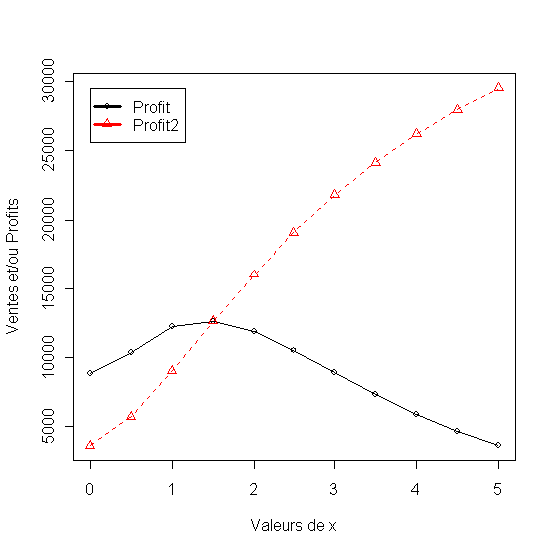
14. matplot(x1, df[,3:4], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
15. legend(min(x1), max(df[,3:4]),names(df)[3:4], lwd=3, col=1:2, pch=1:2)
La figure montre un profit optimum quand l'elasticité au prix dépend du niveau de la publicité et un profit croissant quand l'elasticité au prix est fixe et correspond à l'elasticité calculé précédement pour une publicité optimale de 1.5, ce qui explique que les deux courbes du profis ce croisent à ce niveau de publicité.
Figure 39 - Evolution de profit en fonction de la publicité selon que l'élasticité prix s'acccroît avec la publicité ou non.
- Modèle de l`usure de la publicité [ 5.4-5]
Listing 36
1. # Modèle de l`usure de la publicité
2. a=10
3. b=10
4. c=-1
5. t<-1:10
6. bt<-b*exp(-0.07*(t-1)) # effet d`usure sur le coef b de la pub
7. xopt<-(1-0.3*b)/(0.6*c) # pub optimum ingorant l`usure
8. x<-rep(xopt,10)
9. y<-a+bt*x+c*x^2
10. profit<-0.3*y-x
11. df<-data.frame(Temps=t, Profit1=profit)
12. xopt_t<-(1-0.3*bt)/(0.6*c) # pub optimum utlisant l`usure
13. x<-xopt_t
14. profit<-0.3*y-x
15. df$Profit2=profit
16. df
17. matplot(t, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
18. legend(mean(t), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)
En égalant à zéro la dérivé de la fonction du profit on déduit le budget de publicité optimum à pratiquer. Quand l'usure de la pub qui affecte dans ce cas le coefficient b est ignoré le niveau de publicité optimum reste fixe dans le temps et depend des coefficients initiaux du modèle.
Quand l'usure est prise en compte la publicité optimum n'est pas fixe elle dépend de l'usure dans ce cas du changement dans le temps du coefficient b (qui devient bt). La prise en compte de l'usure a chaque période quand on fixe le budget de publicité à un effet favorable sur les profit tel que l'illustre la figure.
Figure 40 - Profits d'un politique qui prend en compte l'usure la publicité comparée à une politique publicitaire qui prévoit des dépenses constantes.

- Budget optimum quand l interaction des variables du mix et positive, negative ou zero [5.6-9]
Listing 37
1. # Variation du budget optimum quand l interaction des variables du mix et positive, negative ou zero
2. a=50
3. b=200
4. c=2
5. d=2
6. x1<-seq(6,7.9,0.1)
7. x2<-rep(7,20)
8. f1<-a+(b-a)*x1^c/(d^c+x1^c)
9. f2<-a+(b-a)*x2^c/(d^c+x2^c)
10. y<-f1+f2 # sans interaction
11. profit<-0.3*y-x1-x2
12. df<-data.frame(Effort=x1, Profit.InteractZero=profit)
13. y<-f1+f2+0.001*f1*f2 # interaction positive
14. profit<-0.3*y-x1-x2
15. df$Profit.InteractPos<-profit
16. y<-f1+f2-0.001*f1*f2 # interaction negative
17. profit<-0.3*y-x1-x2
18. df$Profit.InteractNeg<-profit
19. df
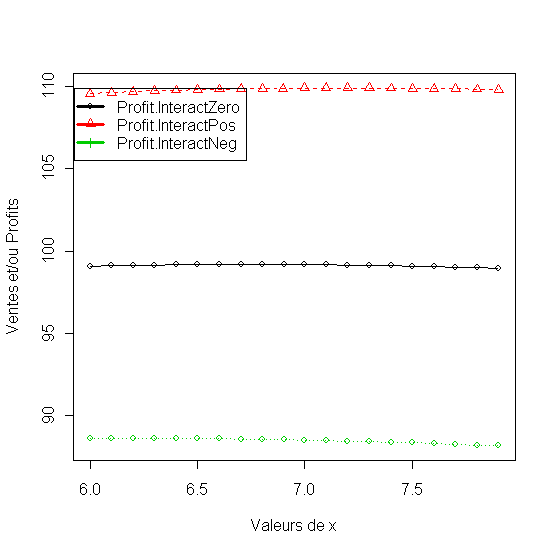
20. matplot(x1, df[,2:4], pch = 1:2, type = "o", col = 1:3,xlab="Valeurs de x", ylab="Ventes et/ou Profits")
21. legend(0.75*max(x1), max(df[,2:4]),names(df)[2:4], lwd=3, col=1:3, pch=1:3)
Figure 41 - Profits quand l'interaction des variables du mix et positive, negative ou zero