Un modèle de réaction à la publicité
Le modèle BRANDAID (Little, 1975) dans sa partie destinée à la publicité par d'un niveau de ventes de référence Vo et postule qu'il existe un taux de publicité po (taux de référence) qui maintiendra ce niveau de ventes. Il suppose aussi que les réaction à long terme vers r(a) des ventes à un certain taux de publicité (index) a(t) = p(t)/po (ou p(t) est le taux de publicité au temps t il est fonction du budget publicitaire, l'efficacité média et du rendement de la création publicitaire) tende des valeurs asymptotiques données par l'expression:
r[a(t)] = k (1- e-b a(t)) + c
La dynamique du processus est donnée par les expressions suivantes:
e(t) = a e(t-1) + (1-a ) r[a(t)]
V(t) = Vo e(t)
ou V(t) sont les ventes à l'instant t
pour intégrer l'effet de la mémorisation sur l'index publicitaire a on peut redéfinir a(t)
a'(t) = b a'(t-1) + (1-b ) a(t)
Exemple pour le tableur:
r[a(t)] = 2,5 [1 - e-0,25 a(t)] + 0,45
Exemples
- Modèle pblicitaire - Stratégie de publicité constante [ 4.17-21.1]
- Modèle pblicitaire - Stratégie de publicité par impulsions [ 4.17-21.2]
Les deux modèles font jouer les effets dynamique (effet imediat lambda et effet à long terme terme alfa). Les deux stratégies sont: Stratégie 1 (pub const.) 1,2 par période; Stratégie 2 (pub par impulsions) dépenses de pub alternavites: 1,4; 1; 0; ...
Listing 31
1. # Effets dynamiques
2. alpha1=0.8
3. lambda=0.2
4. # Modèle pblicitaire 1
5. print("Stratégie de publicité constante")
6. at<-rep(1.2,10) # pub constante
7. rat<-2.5*(1-exp(-0.25*at))+0.45 # réaction à long terme des ventes à la pub (index)
8. S0=100 # Ventes initiales
9. et=rep(1,10)
10. for(i in 2:10)
11. et[i]=alpha1*et[i-1]+lambda*rat[i] # indice d`effet de la publicité
12. St=S0*et # Ventes par periode
13. df<-data.frame(Temps=1:10, Ventes=St)
14. # Modèle pblicitaire 2
15. print("Stratégie de publicité par impulsions")
16. at<-rep(c(1.4,1),5) # pub par impulsions
17. rat<-2.5*(1-exp(-0.25*at))+0.45 # réaction à long terme des ventes à la pub (index)
18. S0=100 # Ventes initiales
19. et=rep(1,10)
20. for(i in 2:10)
21. et[i]=alpha1*et[i-1]+lambda*rat[i] # indice d`effet de la publicité
22. St=S0*et # Ventes par periode
23. df$Ventes2=St
24. df
25. matplot(df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits"
26. legend(1, max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)
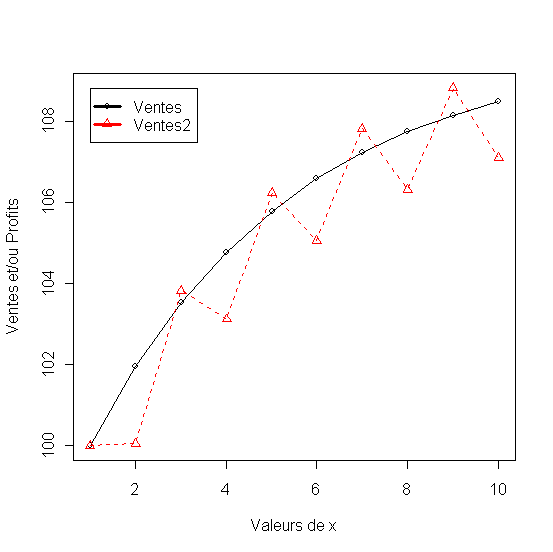
Figure 35 - Comparaison de l'efficacité des politique de dépenses publicitaires: constantes et par impulsions