La triangulation de Delaunay

La triangulation des points éparpillés dans un plan, a fait l'objet d'importantes recherches durant ces dernières décades (Fang et Piegl, 1992). Les origines remontent à Voronoi (1907, 1908) et Delaunay (1932, 1934). De nombreux ouvrages et articles ont présenté les propriétés et les algorithmes utilisés pour la construction de telles triangulations.

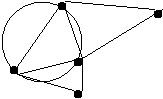
La triangulation de Delaunay semble constituer la structure géométrique la mieux adaptée pour développer un appareil exploratoire (versus normatif) de gestion des aires de marché basé sur la théorie des places centrales. Elle réunit les points les plus proches dans des triangles de telle manière que le cercle qui les circonscrit ne contienne aucun autre point dans l'ensemble (Fig.3 a).

 

Fig. 3 - La triangulation de Delaunay et les polygones de Voronoi

Pour la gestion des points de vente, cela signifie que chaque triangle et son cercle circonscrit,  identifient une zone concurrentielle dans laquelle les trois protagonistes impliqués (dans le triangle) démarquent leurs territoires par des perpendiculaires sur les côtés du triangle. Ainsi, se définit autour de chaque noeud du réseau triangulaire le contour d'une aire de marché polygonale (figure 3 b).