Congruence des aires de marché
Un test peut être effectué pour évaluer la concordance entre les aires de marché réelles ou obtenues par une étude empirique et les aires de marché géométriques déterminées selon nos méthodes de calcul. Le tableau suivant présente une mesure de concordance spatiale.
Indicateur de congruence des zones de marché adapté de Huff et Rust (1984):
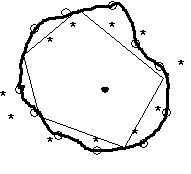
Huff et Rust comparent deux aires de marché calculées pour les mêmes points de distribution et par la même méthode pour tester si les aires de marché varient en fonction des produits, des jours de la semaine ou des périodes dans l'année. Dans notre cas, nous serons amenés à comparer des aires de marché calculées par deux méthodes différentes, une géométrique et discrète (la nôtre) et l'autre empirique et continue a base de courbe spline[5] (méthode de Huff et Batsel, 1977). Il s'agit de proposer quelques traitements préliminaires sur les aires géométriques calculées par notre méthode pour assurer une concordance avec le caractère courbé des aires de marché de Huff et Rust 84, ou Huff et Batsell 1977. Les dernières correspondent à des courbes de niveau qui délimitent un pourcentage donné de la clientèle d'un magasin. En relief cela donne une forme conique irrégulière (semblable à une montagne) ayant le sommet au point de distribution. Nos polygones expriment l'intersection d'une forme conique régulière (le cône de la demande de la théorie des places centrales) ayant le sommet dans le point de distribution avec d'autres formes de ce type exprimant la demande autour de chaque point de distribution voisin. Des arcs de cercle tracés à partir du point de distribution passant par les sommets du polygone (que nous avons calculés) et bornés par les médianes des deux cotés adjacents au sommet (fig.13 a) rendraient ces aires comparables avec les courbes de niveau de Huff et al. C'est sur cette transformation géométrique des polygones qu'on pourra calculer les points extrêmes j qui résultent des intersections tracées avec des angles j à partir du point de distribution. Les angles j sont les angles que forment les points extrêmes (représentés en fig.13 a par "*") constatés dans l'étude empirique par rapport au point de distribution. Connaissant les points extrêmes (représentés par des "o") des nouvelles aires géométriques, on peut utiliser la technique des splines cubiques pour obtenir des aires de marchés continues (fig.13 b). Cette aire de marché sera comparée avec l'aire de marché tracée à partir des points empiriques toujours avec des splines cubiques (fig. 13 c).
|
|
|
|
|
(a) |
(b) |
(c) |
Fig.13 - Construction d'une aire de marché continue autour du point de distribution à partir du polygone et comparaison avec l'aire vérifiée sur le terrain empiriquement; (a) "o" intersections des angles j des points extrêmes empiriques "*" avec les arcs de cercles, (b) aire géométrique - spline passant par les "o" ; (c) aire empirique spline passant par les "*"
Le coefficient de correspondance U des aires obtenues par les deux méthodes serait:
U = ou i = 2i/k (2)
et RE(i) et RG(i) sont les rayons à l'angle i pour les aires de marché obtenues par les deux méthodes (E pour empirique et G pour géométrique). Ce coefficient constitue une mesure globale de la congruence des frontières des deux aires de marché. Pour U zéro la congruence serait parfaite et pour U proche de un il n'y aurait pas de congruence. U2 peut être décomposé en plusieurs indicateurs: un qui mesure la différence de surface entre les deux aires, un autre qui mesure les différences des écarts types des rayons et un qui indique la mesure dans laquelle les deux aires ont la même forme et orientation (pour une discussion détaillée voir Huff et Rust 1984)