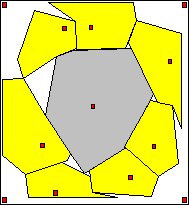
Croisement de perpendiculaires (sans recoupements)

Pour obtenir des aires de marché géométriquement correctes dans des conditions de variation libre de la répartition des points de ventes et des différences d'attractivité, on peut utiliser des perpendiculaires sur les côtés du triangle de Delaunay.

Le point de vente est traité comme un noeud qui réunit tous les triangles adjacents. L'aire de marché autour du noeud est calculée en croisant dans chaque triangle les perpendiculaires sur les cotés adjacents au noeud, qui passent par la limite d'attractivité.

La première solution évite les recouvrements des aires de marché. Elle laisse en revanche des zones non couvertes (no mans land).

Fig. 8  - Aires de marché obtenues par une méthode itérative qui n'admet pas les recouvrements: (a) le point central a une attractivité égale à ses voisins; (b)  le point central a une attractivité supérieure à ses voisins; (c)  le point central a une attractivité inférieure à ses voisins