Utilisation du terme de Lagrange

Pour contourner cette difficulté, on ajoute à l'expression de la variance la condition f'f=k fixant ainsi les valeurs de f et du terme de Lagrange; ce qui donne la fonction:

V = f'Rf-λ(f'f - k).

La variance de la composante est maximum pour

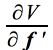= 2 Rf - 2 λ f = 0

d'où l'équation:

(R - λ I)f = 0

Revenons au cas particulier des deux variables; I'expression

(R - I)f = 0

peut s'écrire

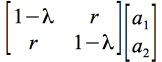= 0

d'où on tire

= 0 et = 0

La seule solution acceptable est celle de l'indétermination, c'est-à-dire de

= = 0

Cette condition détermine, d'une façon générale, le nombre de racines latentes λ possible: ce nombre est égal à l'ordre de R.