Dans un espace à deux dimensions, chaque sujet est représenté par un point dont les coordonnées sont les scores (figure 1).
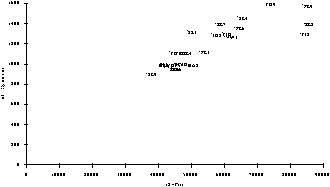
Figure 1. Nuage de points pour deux variables
|
|
L'analyse en composantes principales a pour objet la description synthétique de tableaux de données dans lesquels des individus sont décrits par des variables quantitatives multiples. Cette description doit permettre : - une réduction de l'information; les variables descriptives sont regroupées au sein de facteurs synthétiques, les composantes principales, qui correspondent à des dimensions sous-jacentes du problème; le positionnement des individus par rapport à ces composantes principales, ce qui peut mettre en évidence des typologies d'individus ainsi que les variables qui ont amené à la création de ces types[1]. L'étude d'un échantillon ou d'une population ne peut prétendre habituellement être complète que si un nombre élevé de variables, appelées critères, tests, ou mesures sont évaluées pour chacun des cas. L'ensemble de ces mesures couvre de façon complète, du moins on l'espère, une partie structurée et connaissable du domaine d'investigation. À première vue, chacune de ces variables pourrait sembler d'égale importance; considérant cependant que plusieurs d'entre elles sont en corrélation, donc redondantes, il est possible de découvrir l'existence d'un plus petit nombre de variables dans un ordre décroissant d'importance, indépendantes (du moins habituellement) les unes des autres et telles que les premières expliquent la plus grande partie de la dispersion. C'est l'objectif que se proposent les divers modèles de l'analyse factorielle et qu'ils atteignent, du moins dans leurs grandes lignes[2].
|
|
|
Voici une situation à deux variables permettant d'illustrer géométriquement le but poursuivi par la recherche des composantes principales. Supposons un ensemble de sujets mesurés sur deux variables. Prenons le cas de différents modèles de voitures. Tableau 1 - Données brutes (A)
|
|
|
Dans un espace à deux dimensions, chaque sujet est représenté par un point dont les coordonnées sont les scores (figure 1).
Figure 1. Nuage de points pour deux variables |
|
|
Pour centrer les données on soustrait de chaque élément d'une colonne du tableau (chaque valeur d'une variable) la moyenne de la colonne (de la variable). Tableau 2 - Données centrées (M)
|
|
|
Le graphique pour les premières deux variables est illustré en figure 2
Figure 2. Données centrées |
|
|
Souvent pour éviter les grandes différences d'ordre de grandeur entre les variables on réduit les donne en divisant chaque colonne du tableau (chaque valeur d'une variable) par l'écart type de la colonne (de la variable). Tableau 3 - Données centrées et réduits (X)
|
|
|
Le graphique pour les premières deux variables est illustré en figure 3:
Figure 3 - Données centrées et réduites |
|
|
La forme générale du nuage de points est celle d'une ellipse si les variables sont distribuées normalement. Une ligne contour d'égale densité permet de mieux voir la distribution de ces points.
Figure 4 - Contour elliptique de deux variables conjointes normalement distribuées Considérons les dispersions des deux variables X (Cylindrée) et de Y (Prix) qui sont mesurées habituellement par les variances, mais qu'on représente ici comme les projections extrêmes des lignes contours. Sur l'axe des X la dispersion va de a à b et sur l'axe des Y, elle va de c à d. On constate que les dispersions sur ces deux axes sont habituellement assez importantes pour qu'on doive tenir compte des deux variables pour expliquer adéquatement la dispersion totale: une explication simplifiée par réduction du nombre de variables ne semble donc pas, à première vue du moins, pouvoir être envisagée dans ces conditions. De plus, on observe une corrélation entre les deux variables: il y a redondance, c'est-à-dire que l'une des variables contient une partie de l'information de l'autre. |
|
|
Considérons maintenant les deux axes de l'ellipse comme nouveaux axes de référence du système. Dans le cas de variables standard, ces nouveaux axes forment un angle de 45° par rapport aux anciens. Cet angle est différent dans le cas de variables non standard.
Figure 5 - Représentation des sujets dans l'espace des axes de l'ellipse. En effectuant une modification des coordonnées des points du nuage afin d'exprimer leurs positions par rapport aux nouveaux axes, on réalise une transformation intéressante. Ces nouveaux axes représentent de nouvelles variables, appelées composantes, fonctions des anciennes variables X et Y et dont la dispersion dans le nuage de points est maximum pour l'une, allant de e à f, et minimum pour l'autre, allant de g à h. Ainsi, la première composante rend compte de la plus grande partie de la variance alors que la deuxième composante, en plus d'être indépendante de la première, joue un rôle d'autant moins important que la corrélation rxy est élevée; le rôle de la deuxième composante peut même dans certains cas devenir négligeable. L'indépendance des composantes ressort de l'orientation de l'ellipse relativement aux nouveaux axes de référence. Le but qu'on se donnait est atteint: une situation décrite antérieurement par deux variables liées l'est maintenant par deux composantes indépendantes dont la première est plus importante qu'aucune des variables et dont la seconde, dans certains cas, peut être négligée. |
|
|
L'importance d'une variable ou d'une composante est donnée par sa variance ou sa somme des écarts à la moyenne. On comprendra mieux intuitivement cet énoncé si on considère qu'à la limite, une variable dont tous les scores sont égaux, c'est-à-dire dont la variance est nulle, est une variable qui n'ajoute aucun renseignement à une situation. La plus grande partie du chapitre portera sur l'analyse de variables standard. C'est le cas le plus universel et celui où toutes les variables sont au départ considérées comme d'égale importance. |
|
|
Les sujets d'un échantillon mesurés sur trois variables liées peuvent être représentés dans un espace à trois dimensions par un nuage de points de forme ellipsoïdale; les lieux d'égale densité constituent des surfaces contours dont toute intersection avec un plan décrit une ellipse; un ballon de rugby plus ou moins aplati donne une bonne idée d'un tel contour. Les trois axes principaux sont perpendiculaires et représentent les trois composantes ordonnées. Ces trois composantes sont indépendantes; de plus la première rend compte de la plus grande partie de la variance du système tandis que la variance expliquée par les deux autres composantes est moindre. Dans certains cas, l'importance des deuxième et troisième composantes peut être faible au point de rendre le système presque totalement explicable par la seule première composante, ou dans les situations moins simples, par les première et deuxième composantes. |
|
|
On peut facilement imaginer la situation où un plus grand nombre de variables est étudié, ce qui entraîne espace multidimensionnel, nuage de points hyper-ellipsoïdal, hyperespace, hyperplan, etc. La méthode des composantes principales est aussi dite des axes principaux, ce qui rend plus explicite le modèle géométrique. Un axe principal dans une ellipse est un segment qui, passant par le centre de l'ellipse, atteint celle-ci perpendiculairement à une tangente. Pour espace à trois dimensions et plus, les mots ellipse et tangente sont remplacés par ellipsoïde et plan tangent. La recherche des composantes principales consiste à déterminer ce qu'on pourrait considérer comme les longueurs (racines latentes symbolisées j) et les directions (vecteur fj des vecteurs latents) des axes principaux. |
|
|
Le tableau simplifié avec 10 observations à 6 variables, ça veut dire que 10 modèles de voitures analysées sont jugés selon six critères. Pour réduire la complexité d'une telle comparaison on va utiliser l'analyse en composantes principales pour trouver un nombre réduit (deux) de composantes principales (indépendantes) qui captent la plus grande partie de l'information et qui remplaceront les six variables, qui souvent sont corrélées entre elles. |
|
|
On calcule la matrice des variances covariances (V = M'M/n) en multipliant la transposée du tableau des données centrées (M) avec le tableau lui même. La matrice V calculée est la suivante: Tableau 4 - Matrice de variances/covariances
Sur cette matrice (V) on calcule les valeurs et les vecteurs propres selon un algorithme connu : |
|
|
Tableau 5 - Vecteurs et Valeurs propres de la matrice V
|
|
|
On calcule la matrice de corrélations (R = X'X/n) en multipliant la transposée du tableau des données centrées et réduites avec le tableau. La matrice R calculée est la suivante: Tableau 6 - Matrice des corrélations (R)
Sur cette matrice (R) on calcule les valeurs et les vecteurs propres selon un algorithme connu : |
|
|
Tableau 7 - Vecteurs et Valeurs propres de la matrice R
|
|
|
La somme de valeurs propres
Figure 6 - Valeurs propres et coudes Ca veut dire qu'on peut sans trop de perte d'information utiliser seulement ces deux composantes comme axes pour représenter le nuage de points et par rapport aux axes de variables utilisées dans les graphiques précédents ces axes sont orthogonales (non-corrélées entre elles). |
|
|
En dessous des valeurs propres sont rangés en colonne les vecteurs propres qui sont les coefficients avec lesquels sont pondérées les variables pour obtenir les facteurs. Pour le vecteurs propres normés a l'unité il s'agit des cosinus des angles que forment les variables avec les axes. Pour voir l'orientation des variables par rapport aux composantes principales ils suffit de placer sur un graphique les coordonnées représentés par les vecteurs propres (voir figure 7) L'orientation des variables par rapport aux axes permet d’interpréter ces axes. Les variables qui sont plus proches du première axe du coté positif comme la vitesse, la cylindrée et du coté négatif le poids/puissance, permettent d’interpréter l'axe comme étant l'axe de performances (techniques..). L'autre axe auquel sont corrélés positivement le volume du coffre et négativement la longueur exprime l'utilité en ville. |
|
|
Les nouvelles coordonnées des observations sur les axes sont calculées conformément à la définition des facteurs ( y = xf) en multipliant le tabeau de données originales (centrées reduite) par la matrice des vecteurs propres, Le nouveau tableau est:
Les coordonnées des modèles de voitures qui ce trouvent dans les colonne du tableau Y qui correspondent au premières deux axes sont illustré dans l'image suivante;
Ainsi on obtient la carte de positionnement des sujets analysés, qui permet d'identifier des groupes et d'essayer d’interpréter le positions des observations. |
|
|
Il est rare qu'une analyse factorielle s'arrête à la détermination des composantes principales ou des facteurs communs. En effet, ces opérations donnent généralement lieu à une matrice des saturations où chaque variable est expliquée par plusieurs sinon toutes les composantes retenues. La définition des composantes est souvent difficile à cause du nombre plutôt grand de saturations élevées, en particulier dans le cas des premières composantes: on appelle composantes générales celles définies par toutes les variables et composantes de groupe celles qui ne le sont que par quelques-unes. Soit un ensemble de quatre variables dont on a extrait les composantes. Les vecteurs de transformation, normés pour leurs racines latentes respectives, constituent la matrice F suivante: |
|
|
Les vecteurs propres normés à l'unité, étant des cosinus des angles que forment les variables avec les axes, leur carrés expriment les contributions de chaque variable à chaque axe, la par (le pourcentage) d'une variable dans l'information apporté par un axe. Tableau 8 - Contributions de variables aux axes factoriels
Les sommes des éléments des colonnes sont égales à un. On ne retient, pour l'illustration en deux dimensions, que les deux premières composantes symbolisées A et B: ce sont d'ailleurs les deux seules dont la variance est supérieure à l'unité, c'est-à-dire à celle des variables. Les proportions de la variance totale expliquées par ces deux facteurs sont respectivement 4,36/7 = 0,62 et 1,12/7 = 0,16; la matrice F" des saturations est ainsi réduite à la suivante:
|
|
|
Ici la somme de carrés par colonne est égale à la valeur propre Tableau 9 - Vecteurs propres normés à la valeur propre
|
|
|
Dans la figure 8 on illustre les positions relatives des composantes et des variables. Les composantes étant indépendantes, on les représente par des axes orthogonaux A et B, tandis que les variables sont disposées comme des vecteurs dont les projections sur les axes A et B sont les saturations. chaque vecteur a pour longueur la racine carrée d'une somme de carrés de ligne de la matrice des saturations.
Figure 8. Longueurs et orientations des quatre variables et des facteurs A et B.
La nature de la composante A est définie par l'apport des sept variables à sa variance; ces contributions sont de 19,3% (0,91^2/4,36 = 0,193) pour la première variable, 18,17% (0,892/4,36 = 0,1817) pour la seconde variable, de 16,6% pour la troisième (-0,852/4,36 = 0,1657), de 1,8% pour la quatrième (0,282/4,36 = 0,018), de 4,5% pour la cinquième (0,142/4,36 = 0,0045) , de 16,6% pour la sixième (0,852/4,36 = 0,1657) et de 19,4% pour la septième (0,922/4,36 = 0,1941). Ces contributions, lorsqu'elles sont importantes, ne permettent d'ignorer aucune des variables: on dit d'une telle composante qu'elle est générale La détermination de sa nature serait cependant plus facile si les saturations fortes étaient moins nombreuses. On arrive à ce résultat en effectuant une rotation des axes de référence jusqu'en une position rendant maximum certaines saturations et minimum les autres. |
|
|
En multipliant les premiers deux axes (colonnes) de la matrice
Tableau
10 - Vecteurs propres normés à la valeur propre après
rotation avec un angle de 90° (
La figure 9 illustre une telle rotation orthogonale:
Figure 9. Projection des variables sur les nouveaux axes de référence . Après rotation selon un angle de 90° (voir tableau 10 comparé au tableau 9), les deux axes ne sont pas les mêmes, car elles constituent de nouvelles combinaisons linéaires des six variables. Comme l'angle de rotation ici est de 90°, l'axe 2 prend les valeurs de l'axe 1 et l'axe 1 prends des valeurs initiales de l'axe 2 avec des signe inversés ce qui correspond a une rotation de 180°. La rotation des axes de référence doit continuer jusqu'en une position rendant maximum certaines saturations et minimum les autres. Les nouvelles composantes sont alors dites de groupe par opposition aux composantes générales d'avant rotation. |
|
|
Un dernier aide à l’interprétation des axes
sont les communauté. Elles expriment la variance de chaque
variable reconstitué à partir des facteurs communs,
c'est à dire les axes retenus. Ce raisonnement découle
du fait que la matrice de variance (V) peut être
reconstituée en multipliant la matrice
En multipliant les premieres k colonnes de cette matrice par leur transposée on obtient un matrice qui reconstitue une partie de la matrice V et qui s'appelle C ou la matrice des communautés
La diagonale principale de cette matrice contient la variance des variables initiales reconstitué à partir des premiers k facteurs (axes). Si l'on retient 2 axes dans l'exemple précédent on obtient la matrice des communauté suivante. Tableau 11 - Matrice des communautés (C)
En comparant les diagonales principales des matrices V et C on constate que la seule variable pour laquelle la variance n'est pas reconstitué dans une proportion de ~ 80% (qui correspond à la part d'information capté par les deux premiers axes) c'est le Volume du coffre. Cela est du au fait que cette variable contribue très peu aux deux premiers axes retenus, car elle représente 71% de l'information de l'axe 3 qui n'avait pas été retenu (voir tableau 8) |
|
|
On a donc vu que la configuration de la structure factorielle n'est pas unique: une matrice de saturations définissant une structure peut être transformée sans en trahir les propriétés mathématiques et les hypothèses fondamentales. Il existe donc plusieurs moyens mathématiquement équivalents de définir les dimensions sous-jacentes à un même ensemble de données. Cependant ces solutions ne sont pas toutes équivalentes quant à leur degré de signification dans un domaine théorique donné; certaines respectent mieux la loi de la parcimonie scientifique, d'autres permettent une meilleure compréhension du domaine étudié. Le chercheur a donc la responsabilité finale du choix du type de rotation à effectuer. En termes géométriques, les résultats recherchés dans une rotation peuvent se traduire ainsi: certaines des variables seront rapprochées de l'un ou de l'autre axe nouveau et auront sur ceux-ci des projections élevées; en même temps, elles feront avec les autres axes un angle voisin de 90° s'y projetant faiblement; le plus petit nombre possible de variables restera également éloigné des axes (voir Kim, dans SPSS. D. 484). En d'autres termes, étant donné un nombre de facteurs expliquant une fraction fixe de la variance, il s'agit de simplifier les lignes (méthode quartimax) ou les colonnes (méthode varimax) en rendant voisines de zéro le maximum de saturations. |
|
|
Il existe plusieurs procédés et critères mathématiques pour effectuer ces rotations. La méthode quartimax, proposée vers 1950 par plusieurs auteurs, consiste à maximiser la variance des carrés; comme cette méthode exige la maximisation de la somme des saturations à la quatrième puissance, on l'appelle quartimax. Une autre méthode proposée par Kaiser en 1958 repose sur la maximisation de la somme des variances des carrés des saturations dans chaque colonne il s'ensuit une augmentation de certaines saturations et la diminution des autres. Cette méthode dite varimax est la plus largement employée. Une troisième méthode, dite équimax, vise à la simplification simultanée des lignes et des colonnes de la matrice des saturations. La rotation orthogonale de type varimax est obtenue au moyen de fonctions trigonométriques en traitant deux composantes à la fois:
La matrice de transformation est bien orthogonale car:
Le traitement par ordinateur se prête à des rotations successives d'angle jusqu'à la satisfaction des critères suivants:
a) rotation varimax:
b) rotation quartimax:
|
|
|
Le but de la rotation des axes est de faciliter l'identification de la nature des facteurs. Cependant la tâche n'est souvent pas facile et requiert une bonne connaissance de la nature des variables soumises à l'analyse factorielle On propose ici un exemple d'analyse emprunté à la géométrie élémentaire. Les résultats étant connus, comme le suggère Thurstone, on peut alors porter son attention sur la stratégie qui permet l'identification des facteurs. L'objet de l'étude est le parallélépipède rectangle dont on veut découvrir les facteurs, c'est-à-dire les éléments géométriques essentiels à sa description. On a choisi de créer 100 boîtes dont les 3 dimensions, longueur (L), hauteur (H) et profondeur (P), devraient se dégager comme facteurs; ces dimensions sont générées de façon aléatoire. Pour ces 100 cas, on crée 1û variables y compris celles des dimensions, que l'on soumet à l'analyse factorielle par la méthode de Hotelling. La matrice de saturations, dont on ne retient que les trois premières colonnes, est la suivante pour les autres détails au sujet de cette application): Matrice de saturations (avant rotation)
On constate rapidement que le nombre élevé de saturations importantes rend difficile l'identification des facteurs. Il peut même paraître étonnant que ces facteurs ne soient pas plus clairement mis en évidence par les trois premières variables: cela provient du fait que c'est en tenant compte des 10 variables que l'identification doit se faire. -Cette matrice de saturations est alors soumise à une rotation orthogonale de type varimax, dont voici les résultats: |
|
|
Matrice de saturations (rotation varimax)
|
|
|
L'examen des trois premières lignes montre bien que les variables L, H et P sont les facteurs: chaque variable explique bien un et un seul facteur. Il est rare qu'en recherche on arrive à identifier à l'avance les facteurs; on se retrouve plutôt en présence d'une série de variables plus ou moins liées, comme le sont par exemple les variables composites 4 à 10 de notre tableau. L'identification de chaque facteur, à partir des saturations, est encore possible à la condition de bien connaître la composition des variables. En toutes circonstances, c'est de la connaissance approfondie des variables que dépend le succès de l'opération d'analyse factorielle; on ne saurait trop insister sur cette partie proprement créatrice de l'analyse où les ressources de connaissance et de réflexion du chercheur sont essentielles: le modèle mathématique et l'ordinateur ont fourni leur aide et ne sont plus d'aucun recours pour cette étape très spécifique au domaine étudié. |
|
|
Il y a un certain nombre de précautions à prendre à l'occasion de l'emploi de l'analyse factorielle. En voici quelques-unes. Quoiqu'en principe les scores factoriels soient indépendants, il n'en est pas toujours ainsi en pratique, spécialement si les communautés ou éléments de la diagonale de la matrice des corrélations sont différents de l'unité. Une autre raison de cette indépendance imparfaite est qu'un score factoriel est obtenu par la combinaison linéaire d'un nombre de variables inférieur à celui du problème original. L'analyse factorielle a pour but d'étudier les corrélations "naturelles" entre plusieurs variables. Si ces corrélations étaient artificiellement obtenues, il ne faudrait pas s'étonner de voir apparaître une configuration artificielle de facteurs: ce serait le cas, par exemple, si une variable additionnelle était une combinaison linéaire d'autres variables, ou encore si les mêmes items apparaissaient dans l'élaboration de plus d'une variable; on rencontre une telle situation dans la construction des diverses échelles du MMPI (voir Shure et Miles, p. 14-18). Il peut arriver que deux variables, dont les saturations sont élevées pour un facteur donné, soient effectivement sans corrélation entre elles. On peut observer une telle situation dans la matrice des saturations avant rotation dans l'article 8.4.2. Il est prudent, au moment de la définition des facteurs, de veiller à ne retenir que les variables qui ont entre elles des corrélations significatives. Il est important de tenir compte de l'homogénéité des sujets. La structure factorielle peut être considérablement affectée par l'âge, le sexe, le niveau socio-économique, l'éducation des sujets. Si l'homogénéité ne peut pas être facilement réalisée, certains auteurs préconisent l'insertion de l'une ou l'autre de ces influences comme variables additionnelles, à la condition de les annuler ensuite par l'emploi de la méthode d'analyse factorielle dite de la racine carrée (voir Nunnally, p. 370-371). On ne retient en général que les composantes principales les plus importantes, c'est-à-dire expliquant la plus grande partie de la variance. Il peut arriver cependant que cette plus grande partie de la variance d'un sous-groupe soit attribuable aux composantes négligées: la discrimination entre ces sujets serait apparente surtout sur ces composantes Cette remarque suggère l'importance que peut revêtir la recherche des composantes principales pour divers sous-groupes de l'échantillon original. Les composantes principales, étant indépendantes les unes des autres, sont plus faciles à interpréter que les variables elles-mêmes. Ce qui ne signifie nullement que cette interprétation est aisée. Habituellement on gagne beaucoup à joindre à cette analyse celles de la régression multiple et de la variance à variables multiples. Il ne faut point perdre de vue qu'une technique d'analyse factorielle n'est que l'application d'un modèle mathématique sur un ensemble de données numériques, dans le but de guider l'exploration préliminaire d'un domaine complexe. On peut dans un rapport de recherche se contenter de ne présenter que les matrices des corrélations et des saturations. Une colonne de la matrice des saturations définit une composante. On ne doit pas cependant interpréter les composantes comme uniquement celles d'un certain nombre de tests; elles sont aussi les composantes de scores sur ces tests Lorsqu'on a défini une composante par l'examen d'une des colonnes de saturations, on peut procéder à sa vérification sur les scores factoriels de certains sujets Un sujet possédant la caractéristique de cette composante doit alors présenter un score factoriel proportionnel On peut procéder de façon plus systématique en regroupant les sujets, puis en les comparant au moyen de l'analyse de la variance Si les mêmes facteurs ou composantes ont été obtenus sur plusieurs échantillons, on peut leur accorder une meilleure confiance L'analyse factorielle est habituellement précédée d'hypothèses, et c'est dans ce cas surtout que les facteurs sont utilisés comme concepts théoriques; sinon les composantes qui ne sont qu'une structure mathématiquement justifiée, risquent d'être difficilement explicables. Le changement des signes d'un vecteur latent (si le signe d'un élément est changé, il faut les changer tous) ne modifie pas les propriétés algébriques de la matrice des saturations. Cependant l'interprétation doit être modifiée; il faut considérer le facteur correspondant comme inversé dans son orientation: par exemple introversion plutôt qu'extroversion, difficulté plutôt que facilité, etc. L'absence chez certains sujets d'un ou de plusieurs scores constitue, comme dans toute étude inférentielle, un problème sérieux. Tous les résultats sont en effet nécessaires au calcul des corrélations. S'il n'y a pas lieu de croire à des absences intentionnelles, on peut se permettre d'ignorer les sujets qui en sont affectés. Le nombre de sujets sur lequel on effectue une analyse factorielle est de toute première importance. Une étude sur k variables donne lieu à (k2 - k)/2 corrélations des variables prise deux à deux: ce qui constitue la matrice de corrélations. La probabilité d'apparition d'une corrélation significative, pour la population dont la corrélation est nulle, grandit avec le nombre de corrélations calculées et la petitesse de l'échantillon. Dans le cas d'un petit échantillon, la matrice de corrélations pourrait facilement, par hasard, être truffée de corrélations très erronées: ce qui aurait pour effet de révéler une structure factorielle fausse. Nunnally recommande en pratique de ne point travailler sur un échantillon qui soit plus petit que dix fois le nombre de variables. L'utilisation de grosses batteries de variables, par exemple les questionnaires interminables, comporte de nombreux dangers. Obéissant au désir de tout savoir le chercheur est tenté de multiplier les variables, sans connaissance raisonnable de leur nature, ce qui conduit à des structures inexplicables. On a vu dans l'article précédent combien l'interprétation est dépendante de la connaissance interne de chaque variable. |
|
|
On a vu que le modèle géométrique de la recherche d'une composante consiste à transformer les coordonnées de points, ou ce qui est équivalent, à effectuer une rotation orthogonale des axes, de telle sorte qu'on en arrive à une variance maximum du premier facteur. Le vecteur de transformation (ensemble des coefficients de saturations d'un facteur) agit sur la matrice des variables de façon à créer une variable nouvelle appelée composante. On considérera dans cet article le cas où une importance égale est attachée à chaque variable, en transformant la matrice M des scores bruts en la matrice X des scores standard. |
|
|
Le vecteur des scores de la composante répond à l'expression y = Xf où f est le vecteur de transformation recherché. La variance de la composante s'écrit: y'y/n = (Xf)'(Xf)/n =f'X'Xf/n = f'Rf Cette variance est maximum pour f répondant à la condition:
2Rf = 0 Rf = 0
|
|
|
Examinons le cas simple, mais généralisable, d'une matrice X à deux variables; la condition du maximum de la variance sera:
c'est-à-dire:
d'où On constate alors qu'une solution sans intérêt (
On constate aussi qu'une solution indéterminée est la conséquence de la condition
C'est une condition rarement rencontrée. |
|
|
Pour contourner cette difficulté, on ajoute à l'expression de la variance la condition f'f=k fixant ainsi les valeurs de f et du terme de Lagrange; ce qui donne la fonction: V = f'Rf-λ(f'f - k). La variance de la composante est maximum pour
d'où l'équation: (R - λ I)f = 0 Revenons au cas particulier des deux variables; I'expression (R - I)f = 0 peut s'écrire
d'où on tire
La seule solution acceptable est celle de l'indétermination, c'est-à-dire de
Cette condition détermine, d'une façon générale, le nombre de racines latentes λ possible: ce nombre est égal à l'ordre de R. |
|
|
A chaque valeur
L'ensemble de ces conditions peut s'écrire: RF = FΛ |
|
|
On a vu que la résolution de l'équation RF =
FΛ
qu'on écrit aussi
|
|
|
1) Rappelons la propriété suivante des vecteurs latents normés à l'unité (le théorème 2 de l'article 2.6.4, Laforge, 1981):
Considérant les relations
et
on voit que
et donc que
Les relations (1) et (2) établissent que la somme des carrés des éléments d'une même colonne de F1 est égale à l'unité, de même que celle des éléments d'une même ligne. Pour la matrice
on aura la somme de carrés des lignes et des colonnes égales à zéro ainsi que 2) Dans le cas d'une norme à i on sait que F'F = Λ Considérant les relations
on voit que d'où
Dans le cas d'une matrice de saturations
Fλ
=
ces relations signifient
|
|
|
1 ) L'application de la matrice de transformation
Les variances de telles composantes sont égales aux racines latentes j. Rappelons que les variances des composantes sont
2) L'application de la matrice de transformation
À la suite du théorème 4 de l'article 2.6.4, on montre que les variances de ces facteurs sont égales aux carrés des racines latentes. On a ici, d'après les relations précédentes, I'expression des variances des composantes:
Pour rendre les variances égales à ce qu'elles sont dans le cas de la transformation unitaire F1 il est nécessaire de les diviser par Λ. On écrit donc
Rapprochant les expressions (3) et (4), on observe donc la relation intéressante suivante entre F1 et Fλ:
On retient donc les relations symboliques Y = Y1 = Yλ Λ-1 On a pu constater, que
3) Les v variables de X sont standard alors que les
composantes ont des variances égales aux racines latentes
v =
On pourra trouver utile dans certains cas de rendre standard ces composantes. Il suffit pour cela de diviser les éléments de chaque composante par l'écart type correspondant λi1/2. D'où les composantes standard seront
C'est souvent cette dernière expression qu'on utilise dans les logiciels stastiques pour établir la matrice des composantes standard ou des scores factoriels standard. Cette opération offre l'avantage de rendre comparables les divers scores d'un sujet et facilite l'identification des composantes. |
|
|
|