Recherche d’axes qui maximisent la variance
Considérons maintenant les deux axes de l'ellipse comme nouveaux axes de référence du système. Dans le cas de variables standard, ces nouveaux axes forment un angle de 45° par rapport aux anciens. Cet angle est différent dans le cas de variables non standard.
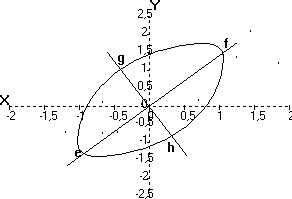
Figure 5 - Représentation des sujets dans l'espace des axes de l'ellipse.
En effectuant une modification des coordonnées des points du nuage afin d'exprimer leurs positions par rapport aux nouveaux axes, on réalise une transformation intéressante. Ces nouveaux axes représentent de nouvelles variables, appelées composantes, fonctions des anciennes variables X et Y et dont la dispersion dans le nuage de points est maximum pour l'une, allant de e à f, et minimum pour l'autre, allant de g à h. Ainsi, la première composante rend compte de la plus grande partie de la variance alors que la deuxième composante, en plus d'être indépendante de la première, joue un rôle d'autant moins important que la corrélation rxy est élevée; le rôle de la deuxième composante peut même dans certains cas devenir négligeable. L'indépendance des composantes ressort de l'orientation de l'ellipse relativement aux nouveaux axes de référence.
Le but qu'on se donnait est atteint: une situation décrite antérieurement par deux variables liées l'est maintenant par deux composantes indépendantes dont la première est plus importante qu'aucune des variables et dont la seconde, dans certains cas, peut être négligée.









