Une rotation orthogonale

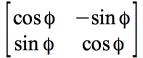En multipliant les premiers deux axes (colonnes) de la matrice par la matrice de rotation on obtient des nouvelles projections qui constituent la nouvelle matrice de saturations (voir tableau 10 )

Tableau 10 - Vecteurs propres normés à la valeur propre après rotation avec un angle de 90° ()

	Axe 1	Axe 2
Cylindrée	-0,04	-1,95
Poids/Puissance	-0,56	1,50
Longueur	-1,58	-0,58
Volume du coffre	0,68	0,43
Consommation	-0,21	-1,31
Vitesse	0,42	-1,72

Quiz Voitures	Plot Voitures
Quiz Camip	Plot Camip

La figure 9 illustre une telle rotation orthogonale:

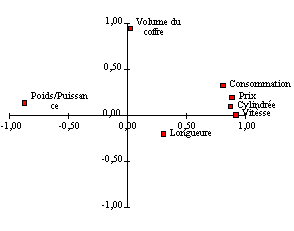
Figure 9. Projection des variables sur les nouveaux axes de référence .

Après rotation selon un angle de 90° (voir tableau 10 comparé au tableau 9), les deux axes ne sont pas les mêmes, car elles constituent de nouvelles combinaisons linéaires des six variables. Comme l'angle de rotation ici est de 90°, l'axe 2 prend les valeurs de l'axe 1 et l'axe 1 prends des valeurs initiales de l'axe 2 avec des signe inversés ce qui correspond a une rotation de 180°. La rotation des axes de référence doit continuer jusqu'en une position rendant maximum certaines saturations et minimum les autres. Les nouvelles composantes sont alors dites de groupe par opposition aux composantes générales d'avant rotation.