Testing Tool learn while playing...

This side shows a little ajax tool that you can use to poke around with the API. Simply select a method, endpoint and add some parameters. Your browser has multiple mechanisms to perform a HTTP request. In most cases you want to do the request using Ajax, which supports all methods. However, Ajax cannot be used for binary streams (e.g. uploading files or displaying images). For those cases you can use the form request method.

Text and Examples

This side shows and overview and descriptions of the API. However OpenCPU is best understood while by playing around with the API.

Whenever you see a red button like the one here, this indicates an example demo. Clicking an example button will automatically fill out the Testing tool and perform the request. Keep your eye on the testing tool while running an example! 


0

					

				


				
			







Analyses univariées


Michel Calciu  


Cours à l'Université de Lille -  2024/2025




Statistiques
  descriptives, Données quantitatives , Mesures de
  position (de tendance centrale)


·  Moyenne
  (arithmétique) 

La moyenne d'une série statistique de n observations est le
  quotient de leur somme par leur nombre.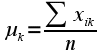 
 Unde k reprezinta coloana iar i linia sau observatia (1) 
















·  Médiane 

La valeur d'une série statistique pour laquelle le nombre
  d'observations inférieures ou supérieures à cette valeur sont
  égal. La détermination de la médiane nécessite le classement de
  la série par ordre de grandeur (croissante ou décroissante). S'il y
  a n = 2p + 1 observations celui de rang p+1 sera la médiane. Si par
  contre n = 2p observations toute valeur comprise entre celle de rang
  p et celle de rang p+1 peut convenir comme médiane. Mesures
  appariées quantile, quartiles(quantile d'ordre 4, Q1,
  Q2 et Q3) et déciles, centile. 

  Mode

Le mode est la valeur la plus souvent rencontrée
  d'une série statistique 



Mesures de dispersion


Definition

Les indicateurs de dispersion ont pour objet de
  mesurer la plus ou moins grande concentration des valeurs autour de
  leur tendance centrale. 

·  Etendue
  (Range) 

La différence entre la valeur maximum et minimum d'une série.
  Est l'intervalle qui sépare les deux valeurs extrêmes 

·  Ecart
  moyen 

est la moyenne des valeurs absolues des écarts par rapport à la
  moyenne; 

·  Dispersion
  ou variation totale 

Est la somme des carrés des écarts par rapport à la moyenne : 
 (2) 

·  Variance 

Est la moyenne des carrés des écarts par rapport à la moyenne :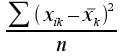 
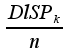 =   = =  (3) 
Si la moyenne a été obtenue sur échantillon, un degré
  de liberté a été consommé pour le calcul de cette moyenne et la
  variance devient 
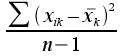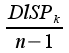 =   = =  (4)  

·  Ecart
  type

Est la racine carrée de la variance : dans le
  cas d'un calcul sur échantillon :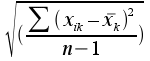 
 =  =  (5) 
















Données qualitatives


Definition

Des données qualitatives apparaissent chaque
  fois que la personne interrogée a le choix entre plusieurs modalités
  qui lui sont proposées explicitement ou implicitement (dans le cas
  d'une question ouverte avec post-codification). 

·  La
  fréquence et la proportion 

Pour chaque individu, la réponse correspond à un code ou
  éventuellement à plusieurs si le choix est multiple (voir
  questionnaire CAMIP). Sur l'ensemble de la population enquêté, on
  dénombrera alors le nombre de fois qu'un code j donné est apparu
  pour la variable k étudiée : ceci indique la fréquence absolue Njk de la modalité. Si cette fréquence absolue est rapportée aux N
  personnes considérées, on obtient la fréquence relative de la
  modalité 
pjk = Njk/N (6) 

·  Variance
  et écart type d'une proportion 

Pour une modalité donnée, la fréquence
  relative joue un rôle similaire à celui de la moyenne pour les
  variables quantitatives. Des Indicateurs de dispersion sont également
  disponibles. Dans la mesure ou un individu a choisi ou non une
  modalité donnée, on a affaire à un processus binomial. Il est donc
  possible d'associer une variance et un écart type à chaque modalité
  d'une variable qualitative : 
VAR(jk) = (pjk) (1 - pjk)/N (7) 
ET(jk) = [(pjk) (1 - pjk)/N]1/2 (8) 
On constate que ces indicateurs sont d'autant plus faibles que pjk est proche de 1 ou de 0. Dans les deux cas, cela signifie que les
  réponses sont très concentrées, soit sur la modalité j, soit sur
  l'ensemble des autres modalités. 

 






     




Données ordinales


Nature

Les données ordinales sont plus difficiles à
  présenter que les autres catégories de données. Comme on l'a vu,
  il s'agit de données concernant des rangs de préférence ou de
  similarité. 
On notera que la notion de rang moyen n'a pas de signification, le
  passage d'un rang au suivant ne correspondant généralement pas a
  une variation d'intensité de préférence constante. 

Quelques mesures

Si l'on prend le cas des préférences, pour chaque individu, on
  disposera d'un classement des m items proposés. Sur l'ensemble de la
  population interrogée, il sera ainsi possible de comptabiliser : 
·  fonction de répartition des rangs 
- le nombre de fois qu'un item donné a été classé en 1re position, en 2e.., en me ; 
·  matrice de préférences. - le nombre de fois qu'un item donné
  a été classé avant un autre item; 

 





     




     












Les intervalles de confiance:
  données quantitatives


Population, échantillons et distribution d'échantillonnage

Dans la plupart des cas, une enquête ne portera
  que sur un échantillon extrait de la population étudiée. On aura
  alors à déduire des résultats obtenus sur échantillon les
  valeurs, c'est-à-dire celles qui seraient disponibles si l'ensemble
  de la population était connue.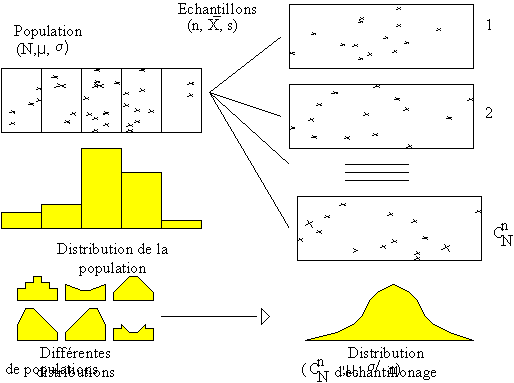 

Figure 1 -
  Population, échantillons et distribution d'échantillonnage 

Théorème Central Limit

Quand on tire des
  échantillons de dimension n d'une population à moyenne µ et variance s2 pour
  des n grands la moyenne des échantillons sera
  distribuée approximativement normalement avec une moyenne égale à µ et une variance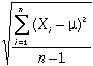 2égale
  à s2/n 
Comme s est inconnu on l'estime
  à partir de s: 
 » =  (9) 

Ajustements pour échantillons exhaustifs

Pour des échantillons exhaustifs quand n/N < 1/7 
(10) 

Distribution normale d'une variable centrée et réduite

Distribution normale d'une variable centrée et réduite Z (m=0 et
  ET = 1) 

  


  

    -3,5 
    -3 
    -2,5 
    -2 
    -1,5 
    -1 
    -0,5 
    0 
    0,5 
    1 
    1,5 
    2 
    2,5 
    3 
    3,5 
  

  

    0,00 
    0,00 
    0,02 
    0,05 
    0,13 
    0,24 
    0,35 
    0,40 
    0,35 
    0,24 
    0,13 
    0,05 
    0,02 
    0,00 
    0,00 
  

  

    0,00 
    0,00 
    0,01 
    0,02 
    0,07 
    0,16 
    0,31 
    0,50 
    0,69 
    0,83 
    0,93 
    0,97 
    0,99 
    1,00 
    1,00 
  







  

   
   
 

   (a) cumulé 
  (b) densité


Figure 2 - La 
  distribution normale d'une variable centrée et réduite



Distribution normale d'une variable


Toute loi normale est complètement caractérisée par ces deux premiers moments centrés : l’espérance et la variance.

   

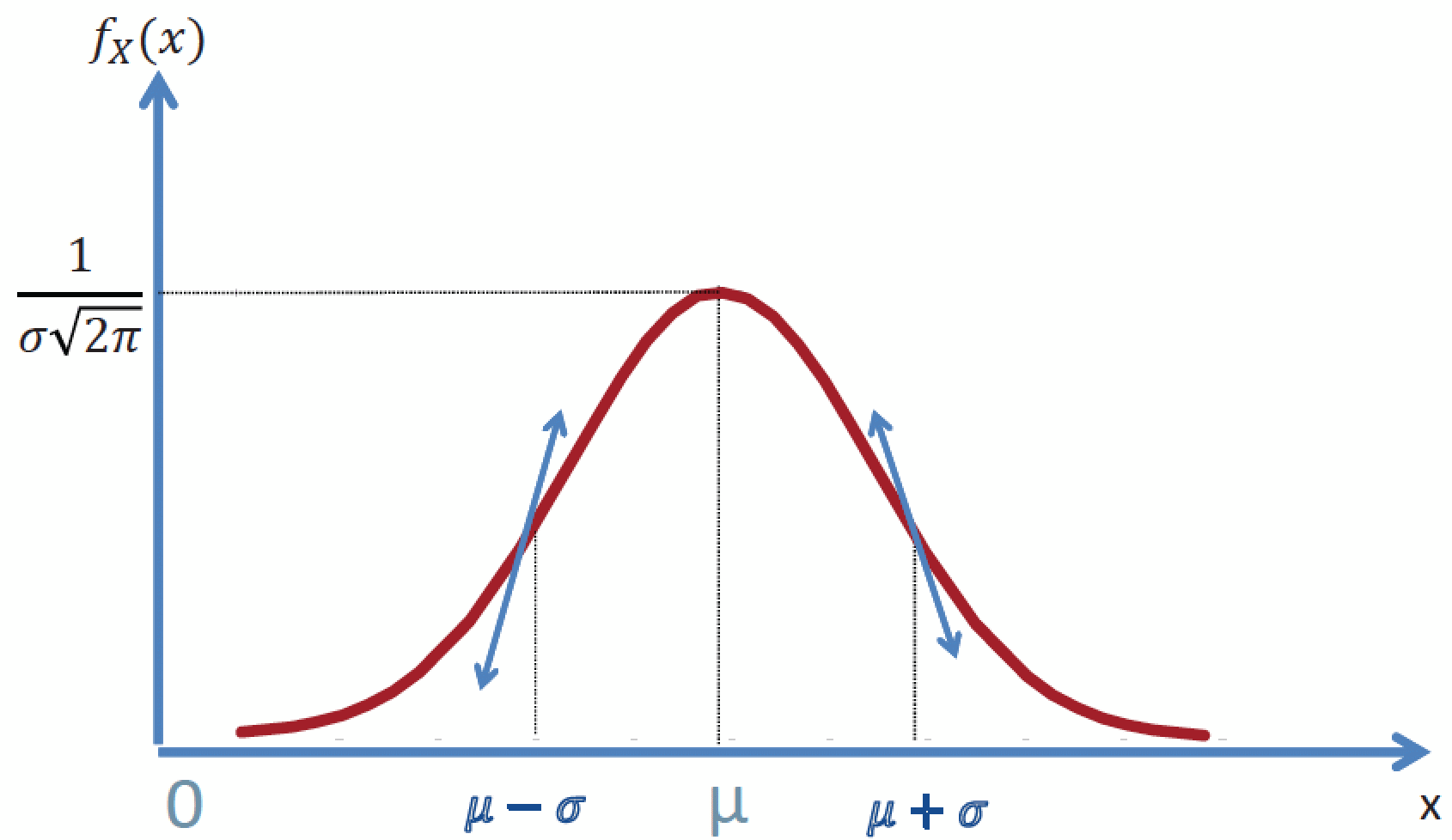
Figure 3 - La distribution normale d'une variable

Si X est une variable aléatoire réelle qui suit une loi normale d’espérance μ et de variance 𝜎2, X ~ N(μ, σ2), alors Z = (X − μ)/σ  ~ N(0, 1)


 Si Z est une variable aléatoire réelle qui suit une loi normale centrée réduite, Z ~ N(0, 1), alors X = μ + σZ  ~ N(μ, σ2)





     




     




     









     




     








 

·  a)
  Détermination de l'intervalle de confiance 

La population totale est de taille N; la valeur vraie de la
  moyenne de la variable analysée est µ, et son écart type s. Ces deux valeurs µ et s sont inconnues, mais sur l'échantillon de taille n, une
  moyenne et un écart-type s ont été repérés (cf. graphique
  1). Il s'agit de déduire µ et s de ces valeurs et s.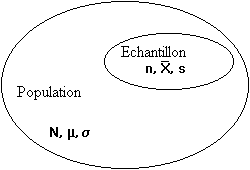 

Figure 4:
  Caractéristiques de la population totale et de l'échantillon 
Cette déduction suit des règles simples issues de la théorie
  des sondages, dans la mesure où les hypothèses suivantes sont
  respectées : 
- les éléments de l'échantillon ont été sélectionnés de
  manière aléatoire; 
- l'échantillon est non exhaustif (n/N < 1/7) 
- l'échantillon comprend au moins 30 individus. 
Dans ces conditions, on montre que les
  moyennes d'échantillon suivent une loi normale de moyenne µ et d'écart type ,
  avec : 
= s /(n1/2) 
Comme s est inconnu, il est
  estimé à partir de s : 
 » = [S(X -)2/(n
  - 1)]l/2 
Si l'on désire travailler avec un seuil de confiance 1-a,
  un intervalle de confiance pour la moyenne µ est obtenu à
  l'aide de l'expression: 
 µ = ± za/2 (11) 
où za/2 est la
  valeur lue dans la table de la loi normale réduite pour une
  probabilité (1 - a/2). Il y a ainsi une
  probabilité (1 - a) que la valeur
  recherchée se situe dans cette fourchette. 




     




     







    
    
    
Exemple

Exemple
L'association des étudiants d'une université envisage d'ouvrir
  un ciné-club; afin d'en évaluer la fréquentation, elle a réalisé
  une enquête par sondage sur un échantillon de 400 individus. 

  Une
  moyenne de fréquentation de 10 séances par an et par individu a été
  obtenue avec un écart type s = 20. Au seuil de confiance (1 - a) =
  95 % l'intervalle de confiance est: 

  µ = 10 ± (1,96) (20/(400)1/2) = 10 ± 1,96 

  Il a 95 chances sur 100 de se situer dans la fourchette
  [11,96: 8,04]. Si l'université comprend 5000 étudiants, une
  fréquentation globale de 50 000 places peut être attendue en
  moyenne; la fréquentation globale a 95 % de chances de se situer
  dans l'intervalle [59800: 40200]. 

Cas particulier: Echantillon exhaustif

1- Dans le cas d'un échantillon exhaustif,
  c'est-à-dire avec n > N/7, l'écart type s,
  des moyennes d'échantillons doit être corrigé par le facteur
  d'exhaustivité [(N - n)/(N - 1)]1/2. L'intervalle de confiance
  devient alors : 
 µ = ± za/2[(N
  - n)/(N - 1)]l/2 (12) 
On remarque que si n est faible par rapport à N, (N - n)/(N - 1)
  est proche de 1. Au contraire, si n est grand par rapport à N, (N -
  n)/(N - 1) est proche de 0; à la limite, pour n = N, µ = . 




 






Exemple

Dans l'exemple précédent, supposons que l'université considérée
  ne comporte que 2 000 étudiants au total. L'échantillon de 400
  personnes prélevé par l'association des étudiants doit donc être
  qualifié d'exhaustif, et il faut utiliser le facteur de correction,
  égal ici à [(2 000 - 400)/(2 000 - 1 )] = 0,80. 

  Au seuil de
  confiance (1 - a) = 95 %, l'intervalle de
  confiance devient: 

  µ = 10 ± (1,96)
  (20/) (0,80)1/2= 10 ± 1,74 µ
  a 95 chances sur 100 de se situer dans la fourchette [11,74: 8,26]. 

Cas particulier: Petit échantillon

2 - Dans le cas d'un petit échantillon,
  avec n < 30, et lorsque s est
  estimé, les moyennes d'échantillons ne sont plus répartis autour
  de la moyenne vraie selon une loi normale, mais selon une loi
  de Student à n - 1 degrés de liberté. Dans la formule
  (1l), za/2 est alors
  remplacé par ta/2,
  lu sur la table de Student pour n -1 degrés de liberté et un seuil
  de confiance (1 - a).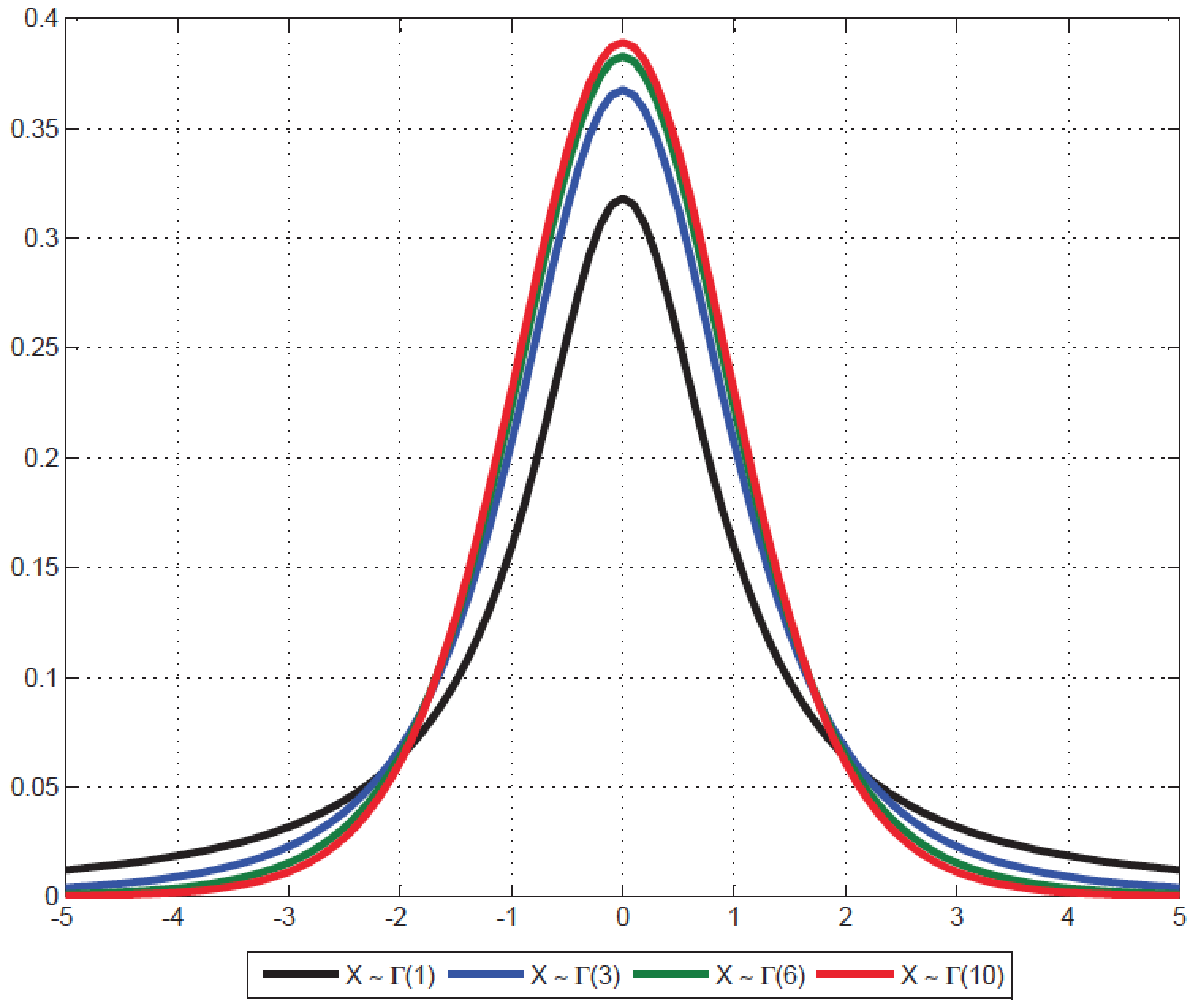 


  

   
   
 

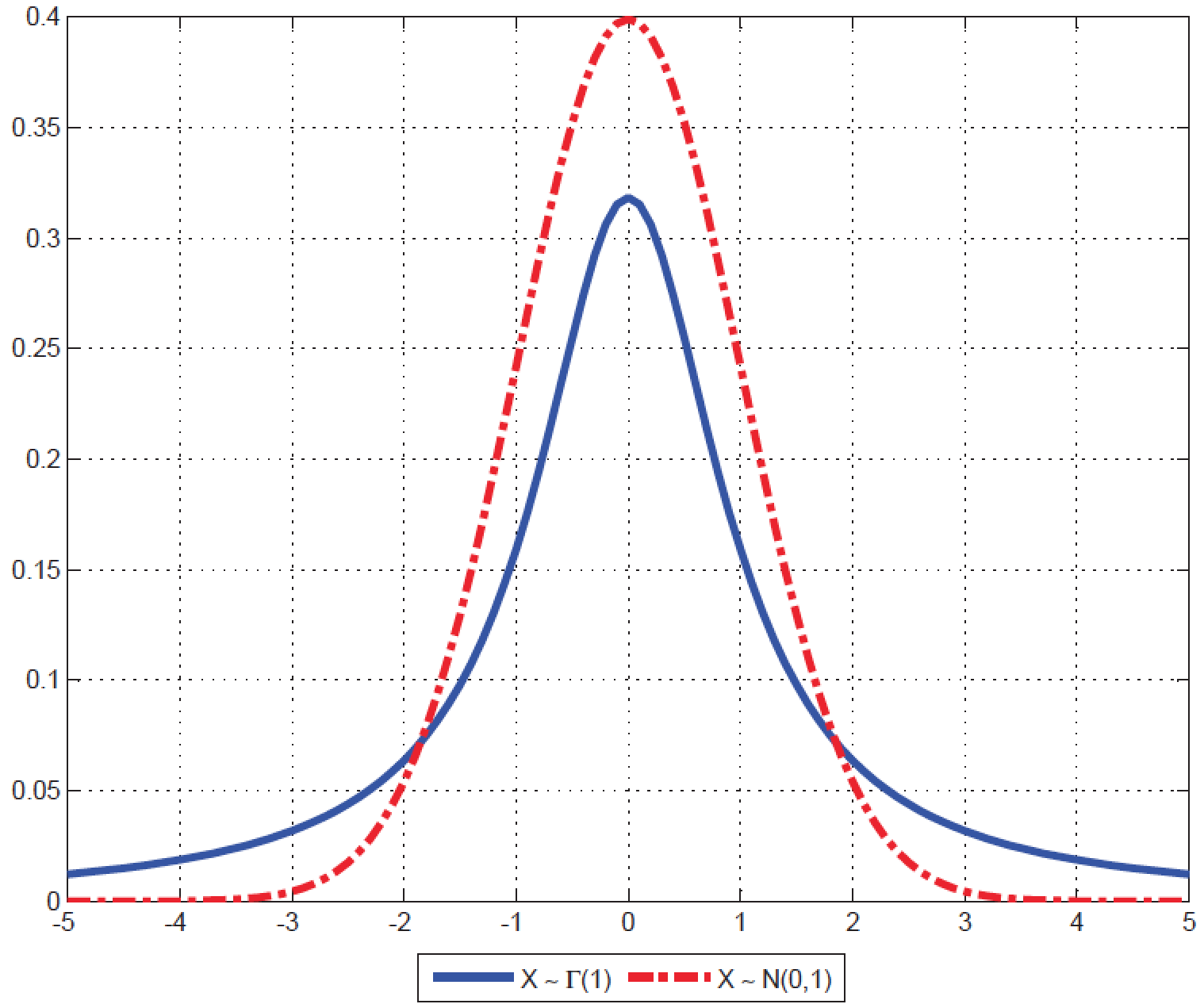   (a) degrés de liberté
  (b) Loi Student vs. Normale


Figure 5 - Loi de Student
  



   
   

   

   

Exemple

Au lieu d'utiliser un échantillon de 400 personnes, L'association
  des étudiants s'est limitée à 21 interviews. La moyenne
  d'échantillon (15) suit une loi de Student à 20 degrés de liberté.
  Dans la mesure où l'écart type repéré sur l'échantillon s'élève
  à 20, au seuil de confiance de 95 %, t = 2,086 et l'intervalle de
  confiance devient alors: 

  µ= 15 ± (2,086) (20/(400-1)1/2) = 15 ± 9,10 à 95 chances sur 100 de se situer dans la fourchette [5,89:
  24,10].




  






Les intervalles de confiance: données
  qualitatives


Particularites

Dans le cas de variables qualitatives, la
  problématique de la prévision des valeurs réelles se pose dans les
  mêmes termes que pour les variables quantitatives, mais maintenant,
  il s'agit de fréquences d'apparition de modalités et non plus de
  moyennes. 
La population totale est de taille N; la valeur vraie de la
  fréquence de la modalité analysée est p.
  Sur l'échantillon de taille n, une proportion p a été trouvée. 

Analogies

On montre que les proportions lues sur les échantillons suivent
  une loi normale de moyenne p et d'écart
  type sp = [p(l - p)/n]l/2. 
Au seuil de risque a, l'intervalle de
  confiance est obtenu par l'expression : 
p = p ± za/2.[p(1 - p)/n]l/2 (15) 
Généralement, on prendra, pour calculer l'écart type des
  proportions, p = 50 %, qui correspond au cas le plus défavorable et
  non la proportion observée.. 




   
   



      
     

     



   




   





Exemple

Dans le cadre d'une étude de notoriété, 25 % des personnes
  interrogées ont déclaré connaître la marque M. Un échantillon
  aléatoire non exhaustif de 1000 individus a été utilisé. L'écart
  type des proportions est alors: 

  [0,5(0,5)/1000]l/2 =
  0,0158. 

  Il y a 95 chances sur 100 que le véritable taux de
  notoriété se situe dans la fourchette: 

  p = 0,25 ± 1,96.(0,0158)

  Il doit être
  ainsi compris entre 0,25 - 0,03 = 0,22 et 0,25 + 0,03 = 0,28,
  c'est-à-dire entre 22 % et 28 %.
  


 





    
 

 

 

Les tests d'hypothèse:
  Données quantitatives


a) Position du problème

(La valeur de la moyenne trouvée sur
  échantillon aura souvent à être mise en relation avec une valeur a priori µo.) On peut faire des
  hypothèses concernant la relation entre la moyenne de la population
  et une telle valeur apriori. Une idée simple est à la base du teste
  d'hypothèses: une Hypothèse peut être rejetée mais elle ne peut
  jamais être acceptée, par ce que des preuve ultérieures peuvent
  montrer le contraire. (exemple: l'homme qui à un comportement
  d'homme pauvre est-il vraiment pauvre...) 

Hypothèse nulle Ho

On appellera Hypothèse nulle Ho l'hypothèse selon laquelle la situation vraie est différente ou
  plus défavorable que celle qui est matérialisée par cette valeur a
  priori. L'hypothèse nulle doit être choisie de telle manière que
  son rejet permet "d'accepter" la conclusion désirée.
  L'hypothèse alternative est Ha. Par
  le biais d'un test d'hypothèse il s'agira d'évaluer dans quelle
  mesure Ho peut être rejetée. 

Test unilatéral et bilatéral

On parlera de test unilatéral quand il
  s'agira de vérifier que la moyenne vraie est plus forte (test dit "
  à droite "), ou plus faible (test dit " à gauche ")
  que µo. On aura affaire à un test bilatéral quand il s'agira de démontrer que la moyenne vraie est différente
  de µo. 

Exemple

Les intentions d'achat X d'un produit nouveau découlant d'une
  enquête par sondage auprès des utilisateurs potentiels doivent être
  comparées avec le seuil de rentabilité de ce produit µo,
  et il faut vérifier l'hypothèse selon laquelle ce seuil de
  rentabilité sera bien dépassé. L'hypothèse Ho s'énonce
  ici de la façon suivante: " la situation du marché est
  telle que le seuil de rentabilité ne sera pas atteint " et H1,: " le seuil de rentabilité sera
  dépassé ". Le test d'hypothèse nécessaire est alors un test
  unilatéral à droite. 

  Si X¯ > µo, ce
  peut être dû au fait que la vraie moyenne est réellement
  supérieure à µo. Ce peut être également dû au fait
  que la vraie moyenne est inférieure à µo mais que le
  hasard a fait porter le sondage sur un échantillon particulièrement
  favorable. Il est évident que plus (X¯  - µo) est grand,
  moins le risque de se trouver dans cette deuxième situation est
  fort.

b) Réalisation d'un test
  unilatéral à droite - 1) Ho : µ < µo

Dans le problème posé, Ho est
  associée à la situation µ < µo. Une première façon
  de procéder consiste à déterminer la probabilité - dénommée probabilité critique p.c. - Avec laquelle Ho est
  conforme aux résultats lus sur échantillon. 
Le graphique 2 résume les termes du problème : Si la moyenne
  vraie était µ, la probabilité d'obtenir sur échantillon une
  valeur supérieure ou égale à serait donnée par la surface lue
  sous la courbe au-delà de la valeur .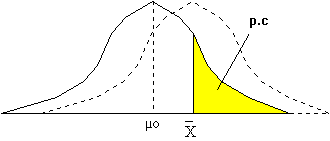 
. 
Figure 6:
  Test unilatéral à droite 
Dans la mesure où le sondage est aléatoire, non exhaustif et
  porte sur un effectif supérieur à 30, cette probabilité est
  calculée à partir d'une table de la loi normale réduite : 
 Z = (-
  µo)/  et p.c. = P (Z* > Z) (13) 
Le fait de rejeter l'hypothèse nulle est associée à un risque
  égal à p.c. Plus cette probabilité critique est faible et moins il
  y a de risque à rejeter Ho. 

2) valeur seuil X*

X*, telle que tout résultat de sondage X
  supérieur à X* permette de rejeter l'hypothèse nulle avec moins de
  chances de se tromper. 
La valeur seuil X* est obtenue à l'aide de l'expression suivante,
  issue de la formule [11] : 
X* = µo + Za (14) 
La règle est alors la suivante: 
• Si < X*: acceptation de Ho 
• Si ³ X*: rejet de Ho 

3) tests unilatéraux à gauche

Les tests unilatéraux à gauche s'effectuent de
  la même façon; la probabilité critique est la surface sous la
  courbe au-dessous de la valeur X trouvée sur échantillon. La
  valeur-seuil X* est calculée à partir de la relation 
X* = µo - Za (15) 
Les tests bilatéraux nécessiteront l'évaluation de deux
  valeurs-seuil: une X* à droite de µo et une X** à gauche, par
  utilisation simultanée des formules (14) et (15). 
  



   
   



   
   



   
   

     


Exemple

Le seuil de rentabilité d'un produit industriel nouveau s'élève
  à 50 en moyenne par entreprise appartenant au marché potentiel Sur
  un échantillon de 100 entreprises, une intention d'achat moyenne de
  62 a été repérée, avec un écart-type de 60. 

  Z62 =
  (62 - 50) / (60/ 1100) = 2 

  p.c. = P(Z > Zx) = p(Z > 2) =
  0,023 

  Avec un seuil de risque a = 5 %, I'hypothèse nulle est
  rejetée. En fait Ho peut être rejetée dès que l'on trouve, sur
  échantillon une valeur au moins égale à: 

  = 50 + (1,64) . (60/
  1001/2) = 59,84 

c) Les risques associés au test d'hypothèse

La procédure qui vient d'être exposée ne
  s'intéresse qu'à une seule catégorie de risque, celui de rejeter
  Ho alors qu'elle est vraie. C'est le risque a ,risque de première espèce ou encore de risque de type 1. Il sera
  souvent nécessaire de prendre également en considération le risque
  d'accepter à tort Ho : c'est le risque b,
  risque de seconde espèce ou encore de type II. 
Le tableau 3 reproduit les résultats possibles d'un test
  d'hypothèse 



	
	
	
	

		
			


			

				
		
			
DÉCISION

				
	

	

		
			
SITUATION REELLE

				
		
			
Ho n'est pas rejetée

				
		
			
Ho est rejetée

				
	

	

		
			
Ho est vraie

				
		
			
Décision correcte 
			

			
Seuil de confiance: 
			

			
Proba = 1 - a 
			

				
		
			
Décision incorrecte 
			

			
Erreur de type I 
			

			
Proba = a 
			

				
	

	

		
			
Ho n'est pas vraie

				
		
			
Décision incorrecte 
			

			
Erreur de type II 
			

			
Proba =b 
			

				
		
			
Décision correcte 
			

			
Puissance du test: 
			

			
Proba = 1 - b 
			

				
	



Tableau 1.3.: Résultats d'un test hypothèse 
Il est bien évident que, pour une taille d'échantillon donnée,
  le risque a et le risque b évoluent de façon opposée. Réduire le risque a demande de choisir
  une valeur-seuil X* plus forte, mais ceci s'accompagne d'une
  augmentation du risque b, puisqu'il y aura
  plus de chances d'accepter à tort l'hypothèse nulle . 

Exemple

Avec les données de l'exemple précédent, on a vu que le risque a était limité à 5 % si l'on
  choisissait une valeur-seuil de 59,84. 

  Supposons que la véritable
  valeur des ventes moyennes par entreprise soit 62. Avec une vraie
  moyenne de 62 et un écart type des moyennes d'échantillon de 6
  (60/1001/2 = 6), il y a une probabilité de 35,94 % de
  sélectionner un échantillon dont la moyenne observée sera
  inférieure ou égale à 59,84. En effet: 

  Z = (59,84 - 62)/6 = -
  0,36 et P(Z £ 0,36) = 0,3594 

  Il y a
  donc ici une probabilité de 35,94 % d'accepter à tort l'hypothèse
  nulle. C'est la valeur du risque b. 

  Si
  l'entreprise veut se prémunir plus fortement contre le rejet à tort
  de Ho avec un risque a de 2,5 % seulement, elle sera amenée à
  choisir une valeur seuil plus forte, égale à: 

  X* = 50 + 1,96(6)
  = 61,76 

  La sélection d'une telle valeur-seuil augmente le risque b. Dans l'hypothèse où la moyenne vraie
  est 62: 

  Z = (61,76 - 62)/6 = - 0,04 et P(Z £ -0,04) = 0,484 

  Le risque b est ici de
  48,4 %.


Pour une illustration voir (ici)
 

Les tests d'hypothèse: Données qualitatives


Analogies

En ce qui concerne les test d'hypothèse, les mêmes procédures
  que pour les variables quantitatives sont employées. C'est la
  formule (15) qui servira désormais dans le calcul des probabilités
  critiques et des valeurs-seuil. 

Exemple

Le taux de notoriété de la marque M dont il était question dans
  l'exemple précédent a été mesuré à la suite d'une campagne
  publicitaire. Le taux de notoriété précédemment connu s'élevait
  à 21%. Peut-on en conclure que la publicité a fait augmenter de
  façon significative la connaissance de la marque ? 

  L'hypothèse
  nulle correspond ici au cas où la publicité n'a eu aucun effet sur
  la notoriété de la marque et donc que la proportion vraie est
  toujours au niveau ancien de 21%. Le rejet éventuel de l'hypothèse
  nulle demande de calculer la probabilité critique p.c., définie ici
  comme la probabilité d'obtenir une proportion observée sur
  échantillon au moins égale à 25 % dans une population où la
  proportion vraie est 21%. 

  La proportion observée p correspond,
  en valeur centrée réduite 

  Zp = (0,25 - 0,21)/0,0158 = 2,53
  probabilité critique est donc: P(Z > Zp) = 0,57 % 
  



   
   



   
   

   

 

    
Les tests de conformité
     avec une distribution théorique


   
Test du chi2

Les résultats du dépouillement d'une question
  qualitative se présentent comme une distribution de fréquences
  d'apparition des différentes modalités de la variable concernée. 
Cette distribution peut être comparée à une distribution a
  priori, dite distribution théorique. Comme dans les tests
  d'hypothèses vus plus haut, deux hypothèses sont alors testées: 
- Ho la distribution observée n'est pas significativement
  différente de la distribution théorique. 
- Hl: la distribution observée est significativement différente
  de la distribution théorique.

La loi du khi-deux


Soient Z1,...
,Zn, n variables aléatoires réelles
indépendantes et identiquement distribuées, Zi
~ N(0; 1), mutuellement indépendantes deux à deux. Alors la
loi de la variable aléatoire définie par : 


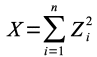est dite loi du khi-deux à n degrés de liberté, 








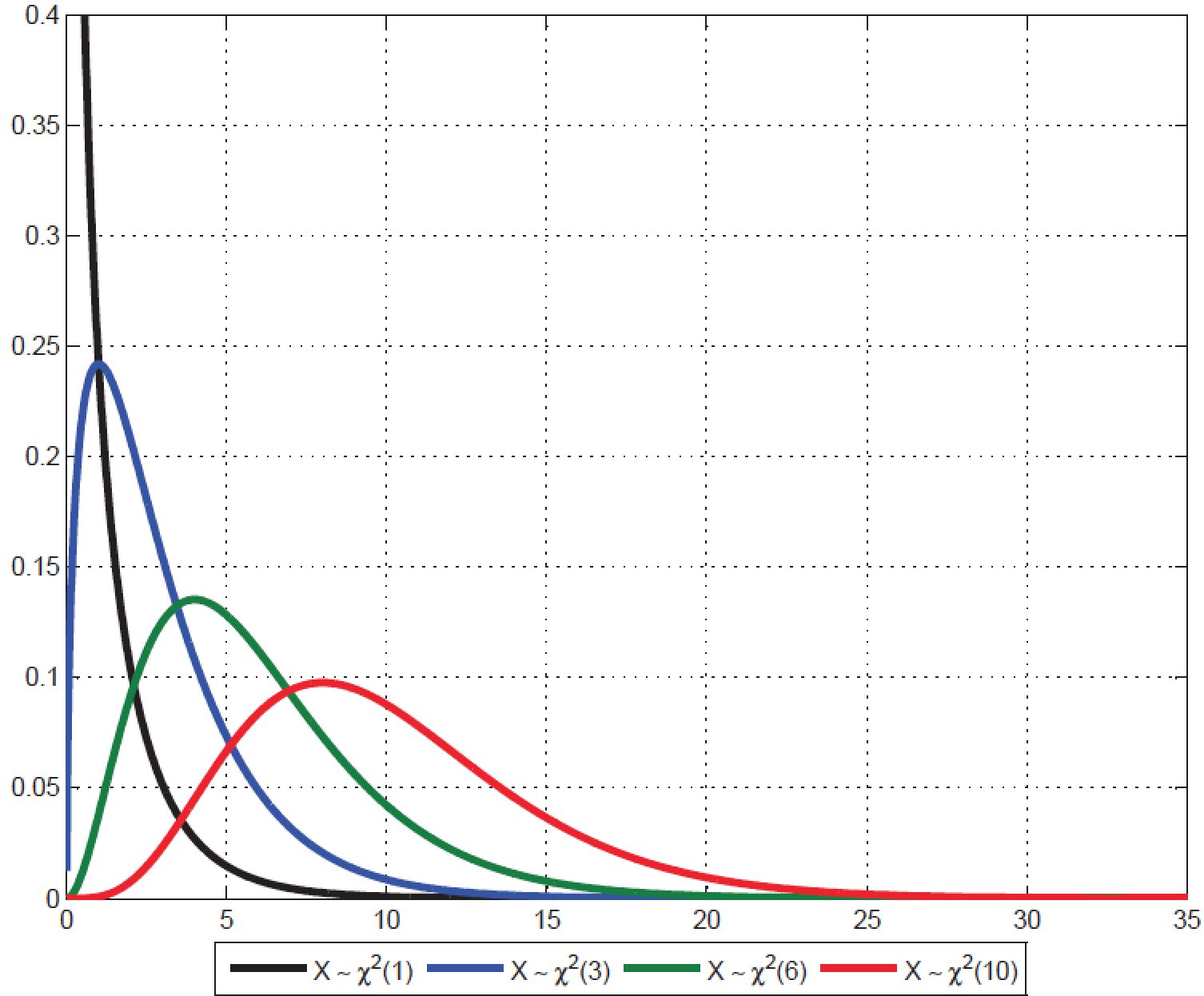
Figure 7 - Loi du
Khi-deux

 



     




     




     






 



     




     







a) Application du test du Khi-Deux

La loi du Khi-Deux (c2)
  donne la répartition des écarts entre les fréquences absolues
  théoriques et les fréquences absolues observées, sous hypothèse
  nulle. 
On mesure le c2 par : 
c2 = S [Nj - qj]2 /qj
  (16) 
où Nj = fréquence absolue observée pour la modalité j; qj = fréquence absolue
  théorique pour la modalité j. 
Cette valeur calculée du c2 est comparée avec la valeur lue sur la table du c2,
  pour m - 1 degrés de liberté lorsque la variable qualitative
  comporte m modalités , et pour un seuil de confiance donné 1 - a.
  Si la valeur calculée du c2 est supérieure à la valeur de la table, Ho peut être rejetée avec
  un risque inférieur à a. 

Exemple

Le tableau 1.4. reproduit une application du test du c2 pour le traitement des résultats d'une étude sur les clients d'une
  ligne aérienne. Il s'agit ici de vérifier si l'échantillon
  interrogé respecte bien les proportions connues des passagers eu
  égard à leur qualité d'abonné ou non. Le c2 calculé apparaissant plus faible que le c2 lu sur la table (5,99 pour 2 degrés de liberté au seuil de 5 %),
  les différences constatées ne sont pas significatives. 
Tableau 1.4.: Application du test du Khi-Deux 


  

     Modalité 
     Effectif observé Nj 
     Effectif théorique Qj
     Nj-Qj;
     (Nj-Qj)2
     (Nj-Qj)2 /Q
  

  

     Abonné année 
     80 
     90 
     -10 
     100 
     1,11 
  

  

     Abonné mois 
     50 
     45 
     5 
     25 
     0 56 
  

  

     Autre 
     100 
     95 
     5 
     25 
     0 26 
  

  

     Total 
     230 
     230 
     
     
     c2=
        1,93
  





Nombre de degrés de liberté: 2 Valeur du Khi-Deux au seuil de 5
  %: 5,99 




  





b) Application du test de Kolmogorov-Smirnov

La qualité de l'ajustement d'une fonction de
  répartition observée à une fonction de répartition a priori peut
  également être évaluée à l'aide du test de Kolmogorov-Smirnov. 
On aura recours à un test chaque fois que les modalités de la
  variable qualitative considérée sont ordonnables, mais aussi
  lorsque les effectifs des différentes classes sont trop faibles pour
  autoriser l'utilisation du test du c2 . 
Le test demande de calculer des fréquence relatives observées
  cumulées Fo(j) et des fréquences relatives cumulées
  théoriques Fq(j) : Fo(j)
  et Fq(j) représentent
  respectivement les pourcentages des effectifs observés et théoriques
  enregistrés jusqu'à la modalité j. Pour chaque modalité la valeur
  |Fo(j) - Fq(j)| est
  calculée. Un indicateur D est alors établi, tel que : 
D = Maxj |Fo(j) - Fq(j)|
  (17) Cette valeur est comparée à celle lue sur une table du D de
  Kolmogorov-Smirnov pour un seuil de confiance donné. A un seuil de
  risque de 5%, et pour des effectifs totaux supérieurs à 35, D est
  approximativement égal à 1,36/ 

Exemple

Le tableau 1.5. donne une application de ce test à l'étude sur
  les clients d'une ligne aérienne. Le D calculé est plus faible que
  le D de la table au seuil de 5% : les différences ne sont pas
  significatives, comme on l'avait déjà constaté avec le test du c2. 
Tableau 1.5.: Application du test de
  Kolmogorov-Smirnov 


  

     Modalité 
     Fréquence 
     Cumulé 
     Fréquence 
     Cumulé 
     |Fo(J)-Fq(J)|
  

  

     
     relative 
     Fo(j) 
     Relative 
     Fq(j)
     
  

  

     
     observée 
     
     Théorique 
     
     
  

  

     Abonné année 
     34,78 % 
     34,78 % 
     39,13 % 
     39,13 % 
     4,35 % 
  

  

     Abonné mois 
     21,74 % 
     56,52 % 
     19,57 % 
     58,70 % 
     2,17 % 
  

  

     Autre 
     43,48 % 
     100,00 % 
     41,30 % 
     100,00 % 
     0,00 % 
  

  

     Total 
     100,00 % 
     
     100,00 % 
     
     
  



Valeur calculée de D = 0,0435 Valeur de D au seuil de 5 %: 0,089