Modèles de prévision et aide à la décision basés sur la réponse en marketing

Michel Calciu calciu@iae.univ-lille1.fr

Cours IAE de Lille 2004

Ce document présente des modèles de prévision et aide à la décision basés sur la réponse en marketing et les méthodes de calcul et traitement statistique qui permettent leur opérationnalisation (1) . Pour les calculs et graphiques on utilise le système R, c'est-à-dire la version « open source » du système S (2) . La concision, l'élégance de son langage ainsi que la flexibilité et capacité de mobiliser des méthodes de calcul des plus simples aux plus sophistiquées nous amène à recommander l'usage de ce système à la place ou en complément du tableur et des logiciels statistiques traditionnels. Le documents est encore en developpement des versions mise à jour seront disponible sur Internet à l'adresse http://claree.univ-lille1.fr/mc_slides/slides_acausal/slides.htm ou http://claree.univ-lille1.fr/cocoon/mc_slides/slides_acausal/slides.htm

Organisation et hiérachie des modèles

Introduction

Le modèle causal
Un modèle causal général pour la réponse en marketing (Lilien 1987):
Un prototype - le modèle ADBUG (Litle, 1970)

Formes des modèles de réponse

Effets statiques

Modèles à une variable explicative

Modèle linéaire
Modèles à paramètres linéaires et variables nonlinéaires

Polynômes
Modèle des séries de puissances
Modèles à racine fractionnelle
Modèles Semi-logarithmique

Modèles nonlinéaires

Modèle Exponentiel Modifié
Modèle logistique
Modèle Gompertz
Modèle ADBUDG

Modèles à plusieurs variables explicatives

Modèle linéaire
Modèles Nonlinéaires
Adjonction d'interaction
Modèles multiplicatifs
Modèles avec transformation logistique

Modèles de part de marché

Modèles multiplicatifs
Modèles d'attractivité
Interaction Competitive Multiplicative (MCI)
Logit Multinomial (MNL)

Effets dynamiques

Modèles de réaction au mix marketing

Modèles de choix des caractéristiques des produits

Modèles de la Valeur Espérée
Régression de la Préférence
L'Analyse Conjointe

Modèles de Prix

Le modèle Classique
Le prix psychologique
Fixation du prix - Etat des connaissances
Prise en compte de la courbe d'expérience

Modèles Publicitaires

Un modèle de réaction à la publicité
La Réaction à la Publicité - Etat des connaissances

Les Modèles de Promotion des Ventes

Un modèles promotionnel

Les Modèles de la Force de Vente

Les Modèles de la Force de Vente

Modèles du mix Marketing

L'interaction du mix
Réaction de la concurrence

Estimation des modeles

Estimation objective

Régression linéaire
Régression non-linéaire

Estimation subjective (decision calculus)

Le modèle causal

Présentation

y = f(xj)

ou y est la variable à expliquer, dépendante

et xj sont les variables explicatives, indépendantes

- Un cas particulier les séries chronologiques

y = f(t)

ou y dépend d'une seul variable le temps

Un modèle causal général pour la réponse en marketing (Lilien 1987):

Qt = ft(Xt, Ct, Et, Qt-1) + et

Qt = les ventes à l'instant t

Xt = les valeurs de variables mix marketing à l'instant t

Ct = les valeurs de variables mix marketing de la concurrence à l'instant t

Et = les valeurs de variables de l'environnement à l'instant t

Qt-1 = les ventes précédentes incorporant les effets passés du mix, de la concurrence et de l'environnement

et = une erreur aléatoire

Un prototype - le modèle ADBUG (Litle, 1970)

Les variables:

X = variables contrôlées par la société (mix marketing)

Q = Ventes de la société

V = Ventes de la concurrence

S = Part de marché (S = Q/(Q+V))

/Q= Potentiel du marché (pour la société)

Exemple réaction des ventes aux dépenses publicitaires:

Tableau 1 - Ventes en fonctions des dépenses publicitaire

publicité (millions francs)	0	1	2	….	n
Ventes (millions unités)	30	40	50	….	60

Application d'un forme simplifiée du modèle ADBUDG (Little, 1970)

Q = 30+30 (2.1 à 2.3)

ou X est le budget publicitaire (Q = a1 + (ao - a1))

Si la marge unitaire est de 0.3 euros le profit sera:

Profit = 0.3*Q(X) - X = marge*Ventes - Coûts Publicitaires

Exemples

Modèle Adbudg initial pour 2Mil. pub 45 Mil. Ventes [ 2.1]
Modèle Adbudg avec inflexion pour 2Mil. pub 55 Mil. Ventes [ 2.2]
Modèle Adbudg accéléré pour 1 Mil. pub 45 Mil. Ventes [2.3]

Listing 1

1.                               a=60
2.                               b=30
3.                               c=1
4.                               d=2
5.                               x<-seq(0,5,1)
6.                               y<-b+(a-b)*((x)^c/(d^c+(x)^c))
7.                               profit<-0.3*y-x
8.                               df<-data.frame(Effort=x, Ventes=y, Profit=profit)
9.                               c=2
10.                             d=3.32
11.                             y<-b+(a-b)*((x)^c/(d^c+(x)^c))
12.                             profit<-0.3*y-x
13.                             df$Ventes2=y
14.                             df$Profit2=profit
15.                             c=1
16.                             d=1
17.                             y<-b+(a-b)*((x)^c/(d^c+(x)^c))
18.                             profit<-0.3*y-x
19.                             df$Ventes3=y
20.                             df$Profit3=profit
21.                             # show Ventes
22.                             matplot(x, df[,seq(2,7,2)], pch = 1:3, type = "o", col = 1:3,xlab="Effort", ylab="Reponse"
23.                             legend(min(x), max(y),names(df)[seq(2,7,2)], lwd=3, col=1:3, pch=1:3)
24.                             # show Profits
25.                             matplot(x, df[,seq(3,7,2)], pch = 1:3, type = "o", col = 1:3,xlab="Effort", ylab="Reponse")
26.                             legend(min(x), max(profit),names(df)[seq(3,7,2)], lwd=3, col=1:3, pch=1:3)

Analyse:

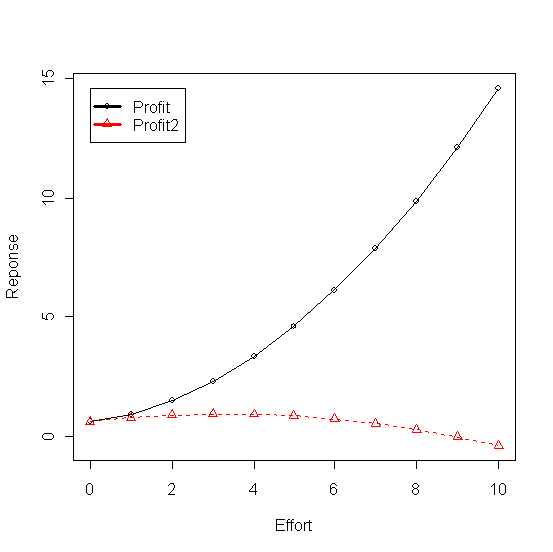
En fixant les coefficients initiaux du modèle a=60, b=30, c=1 et d=2 on calcule les ventes et le profit qui varie entre 0 et 5. En augmentant le coefficient d (d=3.32) on diminue la réactivité du modèle qui se reflètent dans le ventes et dans le profit (Ventes2 et Profit2). Le coefficient c augmenté à 2 a pour éffet d'accroître la valeur du dénominateur par rapport au numérateur quand les x sont petits et de l'inverser ensuite ce qui génre une inflexion et donne au modèle l'allure d'une vraie courbe en "S". En diminuant le coefficient d (d=1) la réactivité du modèle devient supérieure au modèle initiale (Ventes3 et Profit3) et en remettant c=1 le modèle perd sa forme en "S".

Tableau 2 - Ventes et Profit obtenu en faisant varier les coeficients du modèle de réponse (ADBUDG)

  Effort   Ventes   Profit  Ventes2   Profit2 Ventes3 Profit3

1      0 30.00000  9.00000 30.00000  9.000000    30.0    9.00

2      1 40.00000 11.00000 36.94444 10.083333    45.0   12.50

3      2 45.00000 11.50000 41.27820 10.383459    50.0   13.00

4      3 48.00000 11.40000 44.24051 10.272152    52.5   12.75

5      4 50.00000 11.00000 46.39344  9.918033    54.0   12.20

6      5 51.42857 10.42857 48.02885  9.408654    55.0   11.50

Figure 1 - Ventes obtenues en faisant varier les coeficients du modèle de réponse à la publicité (ADBUDG)

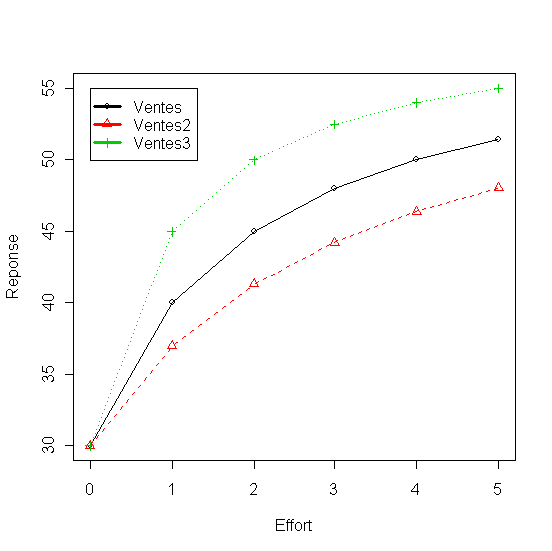
Figure 2 - Profit enregistré en faisant varier les coeficients du modèle de réponse à la publicité (ADBUDG)

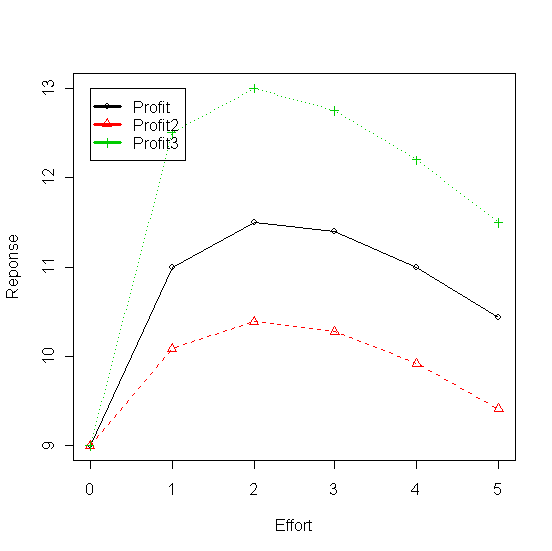
Le graphique montre que la dépense publicitaire optimum avoisine 2 milions de euros.

Critères de classification des modèles de réponse

Le nombre de variables: une ou plusieurs
Forme mathématique de l'interaction des variables: linéaire, non-linéaire (multiplicative, autres)
Statique/dynamique: avec ou sans prise en compte du temps
Effets statiques (les instances de base)

Modèles à une variable explicative

A. - Modèle linéaire

Q =a_o + a₁ X

a1 est la pente de la droite et

ao est la valeur de Q quand X = 0

Forme : linéaire

Réponse marginale : a₁

Limite inf. (X-->0) : a₀

Limite sup. (X-->infinie) : illimité

Exemples :

Modèle linéaire initial [2.6]
Modèle linéaire avec réaction supérieure [ 2.8]

Listing 2

1. x<-seq(0,10,1)

2. y<-2+3*x

3. profit<-0.3*y-x

4. df<-data.frame(Effort=x, Ventes=y, Profit=profit)

5. y<-2+4*x

6. profit<-0.3*y-x

7. df$Ventes2=y

8. df$Profit2=profit

9. df

10. # show Ventes

11. matplot(x, df[,seq(2,5,2)], pch = 1:2, type = "o", col = 1:2,xlab="Effort", ylab="Reponse")

12. legend(min(x), max(df[,seq(2,5,2)]),names(df)[seq(2,5,2)], lwd=3, col=1:2, pch=1:2)

13. # show Profits

14. matplot(x, df[,seq(3,5,2)], pch = 1:2, type = "o", col = 1:2,xlab="Effort", ylab="Reponse")

15. legend(min(x), max(df[,seq(3,5,2)]),names(df)[seq(3,5,2)], lwd=3, col=1:2, pch=1:2)

Analyse:

Deux modèle linéaires sont calculés pour représenter les ventes (y) en fonction des dépenses marketing (x), le première avec une pente de 3 et le deuxieme avec une pente de 4. Même si les ventes representées par le premier modèle augmentent elles sont dépassées par les dépenses ce qui a pour effet la baisse constante du profit. En revanche la pente plus accentuée qu'enregistrent les ventes dans le deuxième modèle (Ventes2) permet de dépasser la croissance des dépenses et offre un profit croissant (Profit2)

Tableau 3 - Croissance linéaire des ventes - les profit baissent quand elle est faible et augmentent quand elle est forte

   Effort Ventes Profit Ventes2 Profit2

1       0      2    0.6       2     0.6

2       1      5    0.5       6     0.8

3       2      8    0.4      10     1.0

4       3     11    0.3      14     1.2

5       4     14    0.2      18     1.4

6       5     17    0.1      22     1.6

7       6     20    0.0      26     1.8

8       7     23   -0.1      30     2.0

9       8     26   -0.2      34     2.2

10      9     29   -0.3      38     2.4

11     10     32   -0.4      42     2.6

Figure 3 Croissance linéaire des ventes (faible et forte)

Figure 4 - Profit en baisse pour des ventes en faible croissance et en hausse autrement

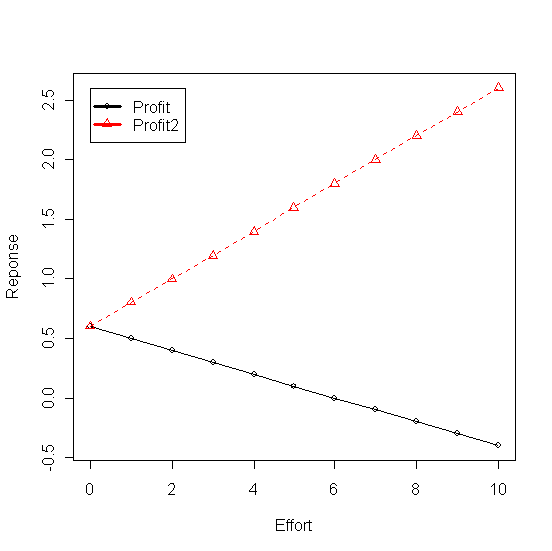
B. - Modèles à paramètres linéaires et variables nonlinéaires

Polynômes

Q = a_o + a₁ g₁(X) + a₂ g₂(X) + .. + a_n g_n(X)

Modèle des séries de puissances

Q = a_o + a₁ X + a₂ X² + ... + a_n Xⁿ

Forme : différentes

Réponse marginale : a₁

Limite inf. (X-->0) : a₀

Limite sup. (X-->0):

Exemples :

Modèle des séiries de puissances a rythme croissant [ 2.12]
Modèle des séiries de puissances a rythme décroissant [ 2.13]

Listing 3

1. x<-seq(0,10,1)

2. y<-+2+4*x+0.4*x^2

3. profit<-0.3*y-x

4. df<-data.frame(Effort=x, Ventes=y, Profit=profit)

5. y<-+2+4*x-0.1*x^2

6. profit<-0.3*y-x

7. df$Ventes2=y

8. df$Profit2=profit

9. matplot(x, df[,c(2,4)], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

10. legend(min(x), max(df[,c(2,4)]),names(df)[c(2,4)], lwd=2, col=1:2, pch=1:2)

11. matplot(x, df[,c(3,5)], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

12. legend(min(x), max(df[,c(3,5)]),names(df)[c(3,5)], lwd=2, col=1:2, pch=1:2)

Analyse:

Le troisième coefficient du modèle affecte la forme de la courbe de réponse. Quand il est positif (ici 0.4) les rendements sont croissants. Quand il est négatif (ici -0.1) les rendements sont décroissants (Ventes2) ce qui est plus réaliste pour une fonction de réponse en marketing.

Tableau 4 - Rendement croissant et décroissant des ventes et leur impacte sur le profit

   Effort Ventes Profit Ventes2 Profit2

1       0    2.0   0.60     2.0    0.60

2       1    6.4   0.92     5.9    0.77

3       2   11.6   1.48     9.6    0.88

4       3   17.6   2.28    13.1    0.93

5       4   24.4   3.32    16.4    0.92

6       5   32.0   4.60    19.5    0.85

7       6   40.4   6.12    22.4    0.72

8       7   49.6   7.88    25.1    0.53

9       8   59.6   9.88    27.6    0.28

10      9   70.4  12.12    29.9   -0.03

11     10   82.0  14.60    32.0   -0.40

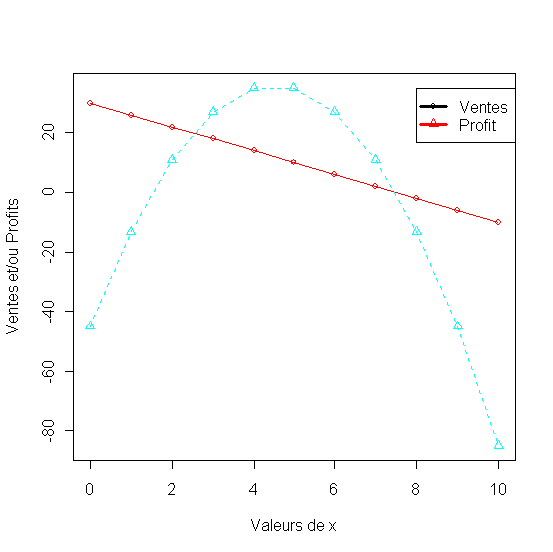
Figure 5 - Ventes à rendement croissant et décroissant

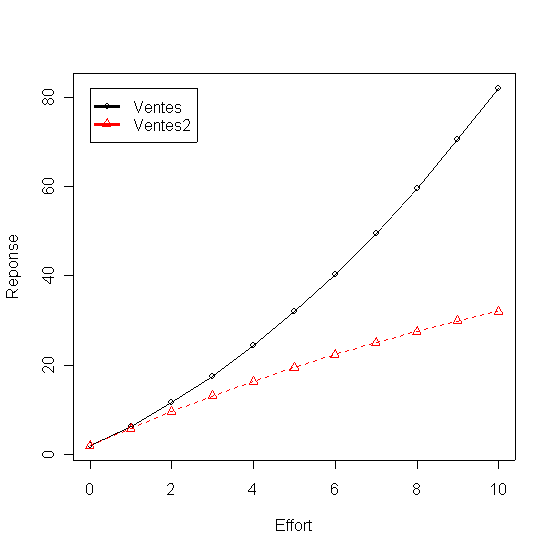
Figure 6 - Profits qui résultent de ventes à rendement croissant et décroissant

Le graphique montre que profit maximal est de 3-4 millions

Modèles à racine fractionnelle

Q = a_o + a₁ X^a2...

Forme : trois allures possibles en fonction de a2: <= -1; (-1; 1); >1

Réponse marginale : ..

Limite inf. (X-->0) : ..

Limite sup. (X-->0) : ..

Exemples :

Modèle de Racine Fractionnelle, rythme décroissant applicable aux prix [ 2.15]
Modèle de Racine Fractionnelle, accroissement à rythme décroissant [ 2.15_2]

Listing 4

1. a=0

2. b=1

3. c=-0.5

4. d=0

5. x<-seq(1,10,1)

6. y<-a+b*(x)^c

7. profit<-0.3*y-x

8. df<-data.frame(Effort=x, Ventes=y, Profit=profit)

9. c=0.5

10. y<-a+b*(x)^c

11. profit<-0.3*y-x

12. df$Ventes2=y

13. df$Profit2=profit

14. df

15. # show Ventes

16. matplot(x, df[,seq(2,5,2)], pch = 1:2, type = "o", col = 1:2,xlab="Effort", ylab="Reponse")

17. legend(min(x), max(df[,seq(2,5,2)]),names(df)[seq(2,5,2)], lwd=3, col=1:2, pch=1:2)

Analyse:

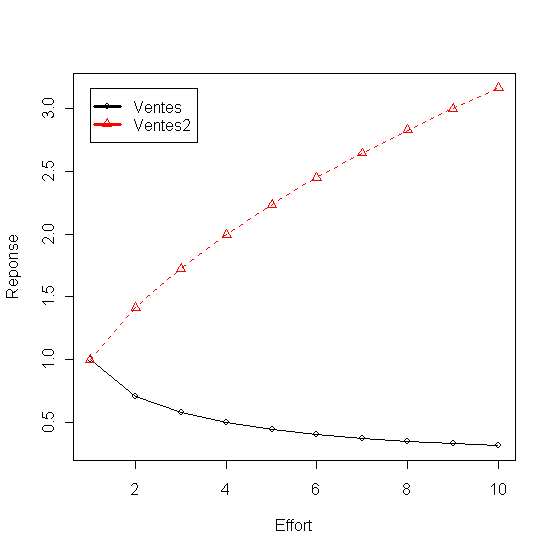
On calcule d'abord un modèle à racine fractionnelle avec un rythme décroissant indique par le coeffcient c (c=-0.5) . Il est applicable aux prix. Quand le coefficient c est positif mais infériur a 1 (ici c= 0.5) on enregistre un acroissement des ventes à rythme décroissant (Ventes2).

Figure 7 - Réponse à rythme décroissant et réponse avec accroissement à rythme décroissant

Modèle de Racine Fractionnelle, rythme croissant [ 2.15_3]

Listing 5

1. a=0

2. b=1

3. c=1.5

4. d=0

5. x<-seq(1,10,1)

6. y<-a+b*(x)^c

7. matplot(x, y, pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

Analyse:

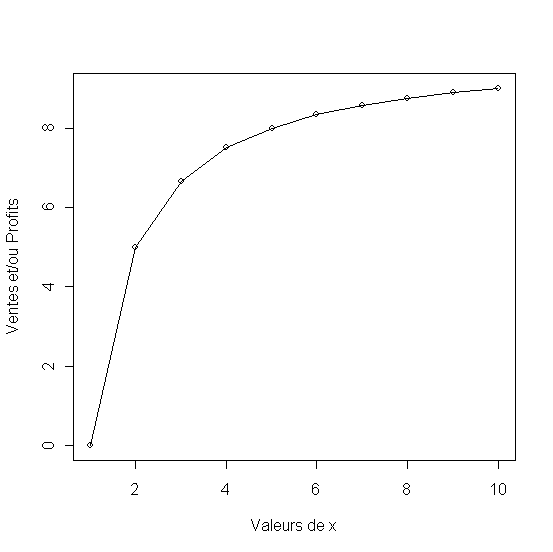
Quand le coefficient c est positif et supérieur à 1 (ici c=1.5) on obtient une réponse à rythme croissant.

Figure 8 - Modèle de réponse à rythme croissant

Modèle de Racine Fractionnelle, equivalent au modèle de saturation [2.15_4]

Listing 6

1. a=10

2. b=-10

3. c=-1

4. x<-seq(1,10,1)

5. y<-a+b*(x)^c

6. matplot(x, y, pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

Analyse

Une forme particulière de réponse obtenue du même modèle de racine fractionnelle, est le modèle de saturation. Dans ce cas le coefficient c=-1. Le modèle devient alors y=a+b/x ou a exprime le niveau de saturation (ici a=10) et b est negatif. Ici b=-a pour que la réponse soit égale à zero quand x = 1.

Figure 9 - Modèle de saturation

Modèles Semi-logarithmique

Q = a_o + a₁ ln(X)

Forme : concave

Réponse marginale : b e^a0/a1 quand x = e^-a0/a1

Limite inf. (X-->0) : 0 quand x = e^-a0/a1

Limite sup. (X-->0) : illimité

Listing 7

1. a=1

2. b=1

3. x<-seq(1,10,1)

4. y<-a+b*log(x)

5. df=data.frame(Effort=x, Ventes=y)

6. a=0

7. y<-a+b*log(x)

8. df$Ventes2=y

9. b=2

10. y<-a+b*log(x)

11. df$Ventes3=y

12. matplot(x, df[,2:4], pch = 1:3, type = "o", col = 1:3,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

13. legend(min(x), max(df[,2:4]),names(df)[2:4], lwd=3, col=1:3, pch=1:3)

Analyse:

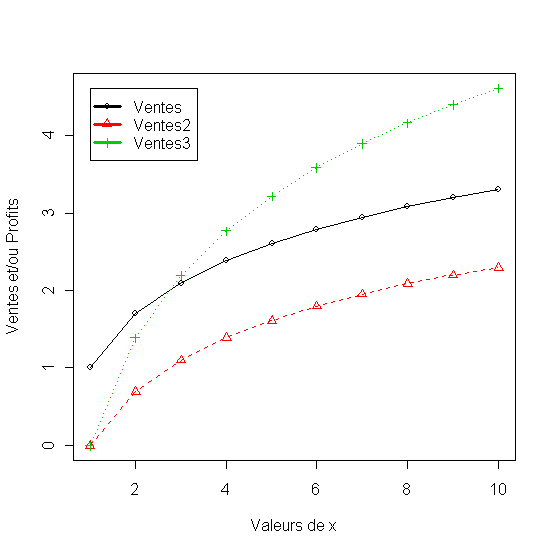
Vue les contrainte imposés par la définition des logarithme ici la valeur minimum de x est 1. La premiere formulation de la réaction de ventes pose a=1 qui indique la valeur minimum de la fonction. Dans les autre deux formulations a=0 d'abord avec b=1 pour donner un deuxième courbe (Ventes2) et ensuite b=2 ce qui imprime au ventes une croissance plus importante (Ventes3).

Figure 10 - Modèle semilogarithmique

C. - Modèles nonlinéaires

Modèle Exponentiel Modifié

Q = a_o(1 -) + a2

Forme : concave

Réponse marginale : a₀ a₁

Limite inf. (X-->0) : a₂

Limite sup. (X-->0) : a₀+a₂

Exemples:

Modèle Exponentiel Modifie, approche lentement la saturation [ 2.17]
Modèle Exponentiel Modifie, approche rapidement la saturation [ 2.17_2]

Listing 8

1. a=10

2. b=0.2

3. c=0

4. d=0

5. x<-seq(0,10,1)

6. y<-a*(1-exp(-b*(x)))+c

7. df<-data.frame(Effort=x, Ventes=y)

8. b=0.4

9. y<-a*(1-exp(-b*(x)))+c

10. df$Ventes2=y

11. df

12. matplot(x, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

13. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Analyse:

Deux forme du modèle sont construites un qui approche lentement la saturation (b=0.2) et un autre qui l'approche plus rapidement (b=0.4)

Figure 11 - Modèle exponentiel modifié

Modèle logistique

Q = + a₃

Forme : forme en S

Réponse marginale : a₀a₂e^-a1/(1+e^-a1)²

Limite inf. (X-->0) : a_0/(1+e^-a1) + a₃

Limite sup. (X-->0) : a₀+a₃

Exemples:

Modele Logistique, approche lentement la saturation [2.18]
Modele Logistique, approche rapidement la saturation [ 2.18_2]

Listing 9

1. a=10

2. b=-2

3. c=0.3

4. d=3

5. x<-seq(0,10,1)

6. y<-a*(1/(1+exp(-b-c*(x))))+d

7. df<-data.frame(Effort=x, Ventes=y)

8. c=0.6

9. y<-a*(1/(1+exp(-b-c*(x))))+d

10. df$Ventes2=y

11. df

12. matplot(x, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

13. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

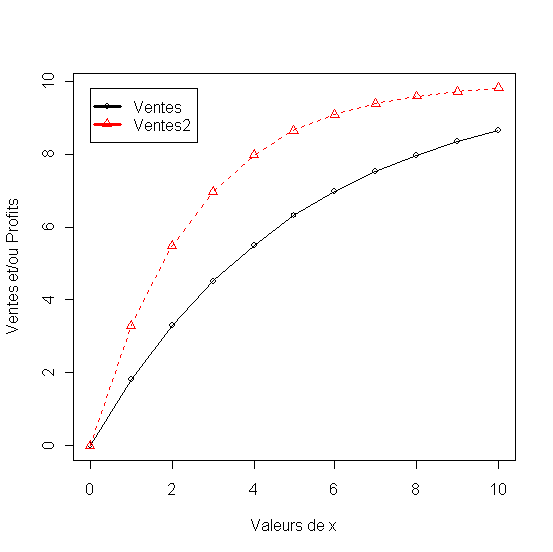
Analyse:

Deux forme du modèle sont construites une qui approche lentement la saturation (c=0.3) et un autre qui l'approche plus rapidement (c=0.6)

Figure 12 - Modèles Logistiques croissants

Modele Logistique, décroissant applicable aux prix [ 2.18_3]

Listing 10

1. a=10

2. b=-2

3. c=-0.3

4. d=3

5. x<-seq(0,10,1)

6. y<-a*(1/(1+exp(-b-c*(x))))+d

7. df<-data.frame(Effort=x, Ventes=y)

8. df

9. matplot(x, y, type="l", xlab="Valeurs de x", ylab="Ventes et/ou Profits")

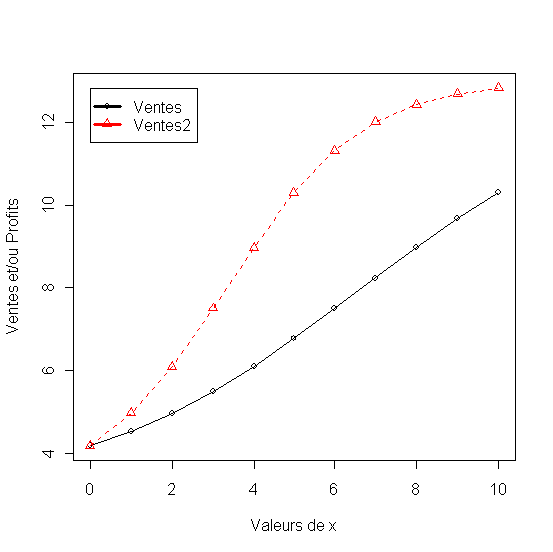
Analyse:

La seule différence par rapport aux formulation précedentes est que le coefficient c est negatif (ici c=-0.3). Cela rend la rend le modèle décroissant et apte pour representer la réponse (Ventes) par rapport aux prix par exemple.

Figure 13 - Modèle Logistique décroissant

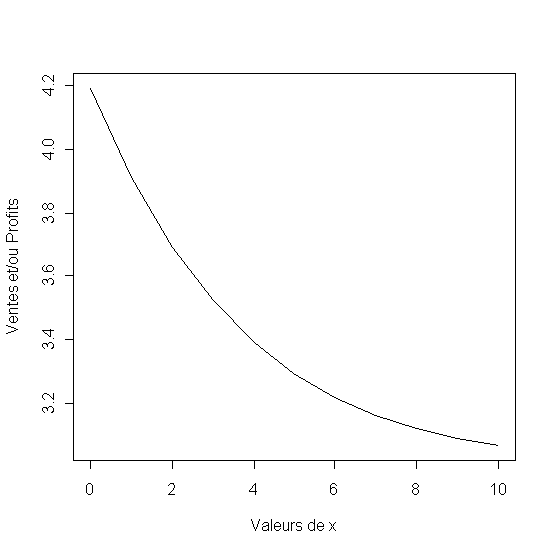
Modèle Gompertz

Q = ao+a3

Forme : S

Réponse marginale : a₀a₁ln(a₂ ln(a₃))

Limite inf. (X-->0) : a₀ a₁ + a₃

Limite sup. (X-->0): a₀ + a₃

Exemples :

Modele Gompertz, approche lentement la saturation [ 2.19]
Modele Gompertz, approche la saturation à une vitesse moyenne [ 2.19_2]
Modele Gompertz, approche rapidement la saturation [ 2.19_3]
Modele Gompertz, modification de l'origine [ 2.19_4]

Listing 11

1. a=10

2. b=0.1

3. c=0.2

4. d=0

5. x<-seq(0,10,1)

6. y<-a*b^c^(x)+d

7. df<-data.frame(Effort=x, Ventes=y)

8. c=0.6

9. y<-a*b^c^(x)+d

10. df$Ventes2<-y

11. c=0.9

12. y<-a*b^c^(x)+d

13. df$Ventes3<-y

14. b=0.2

15. c=0.6

16. y<-a*b^c^(x)+d

17. df$Ventes4<-y

18. df

19. matplot(x, df[,2:5], pch = 1:4, type = "o", col = 1:4,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

20. legend(min(x), max(df[,2:5]),names(df)[2:5], lwd=3, col=1:4, pch=1:4)

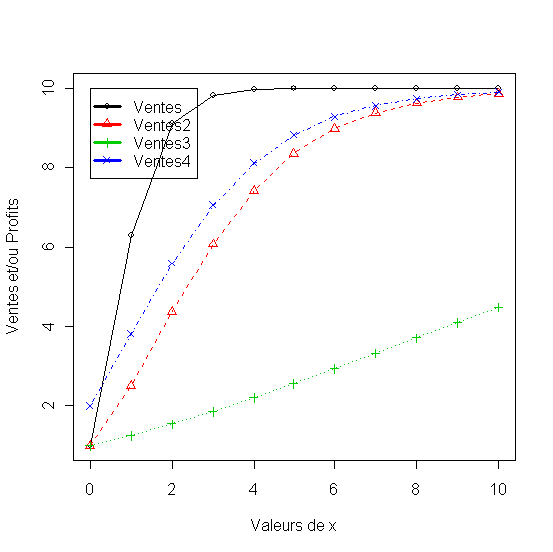
Analyse:

Les premieres trois formulations du modele Gompertz jouent sur l'augmentation du coefficient c. Quand c=0.2, la réponse (Ventes) approche rapidement la saturation. Quand c=0.6 elle approche la saturation à une vitesse moyenne (Ventes2) et quand c=0.9 elle approche lentement la saturation (Ventes3). La modification du coefficient b augmente le niveau de l'origine de la réponse (Ventes4)

Figure 14 - Modèle Gompertz

Modèle ADBUDG

Q = a₁ + (a_o - a₁)

Forme : S quand a₂ >1 et concave autrement

Réponse marginale : 0 pour a₂ >1 et infinie autrement

Limite inf. (X-->0) : a₁

Limite sup. (X-->0) : a_o

Exemples:

Modele Adbudg, approche lentement la saturation [2.20]
Modele Adbudg, approche rapidement la saturation (forme en S) [2.20_2]

Listing 12

1. a=10

2. b=1

3. c=0.5

4. d=2

5. x<-seq(0,10,1)

6. y<-b+(a-b)*((x)^c/(d^c+(x)^c))

7. df<-data.frame(Effort=x, Ventes=y)

8. c=2

9. y<-b+(a-b)*((x)^c/(d^c+(x)^c))

10. df$Ventes2<-y

11. df

12. matplot(x, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

13. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Analyse:

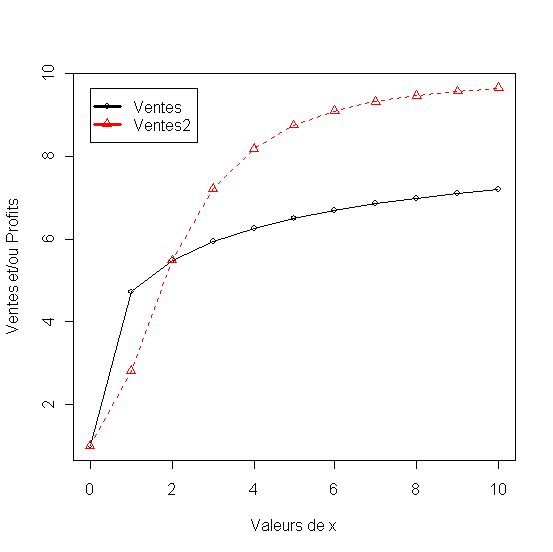
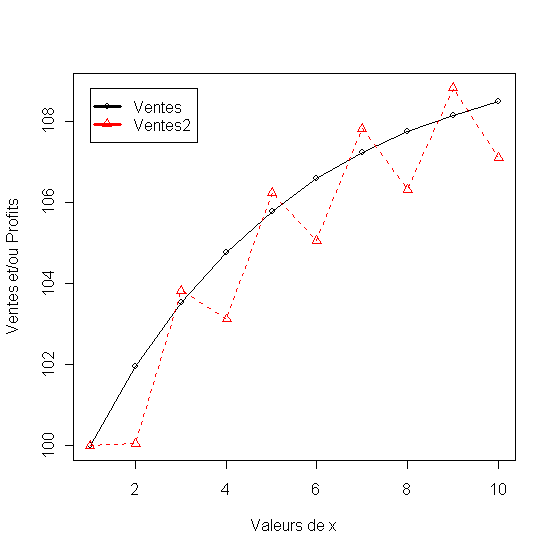
Deux forme du modèle sont construites une (Ventes) qui approche lentement la saturation (c=0.5) et une autre (Ventes2) qui l'approche plus rapidement (c=2)

Figure 15 - Modèle ADBUDG

Modèles à plusieurs variables explicatives

Modèle linéaire

Q = a_o + a₁ X₁ + a₂ X₂ + .. + a_n X_k

Modèles Nonlinéaires

Q = ao + a1 g1 (X1) + a2 g2 (X2) + .. + ak gk (Xk)

Exemples :

Modele Adbudg, lègèrement plus sensible à la publicité qu'à la force de vente [ 2.21]
Modele Adbudg, lègèrement moins sensible à la force de vente qu'à la publicité[ 2.21_2]

Listing 13

1. a=10

2. b=0

3. c=2

4. d=2

5. x<-seq(0,10,1)

6. y<-b+(a-b)*((x)^c/(d^c+(x)^c))

7. df<-data.frame(Effort=x, Ventes.ForceV=y)

8. d=1.5

9. y<-b+(a-b)*((x)^c/(d^c+(x)^c))

10. df$Ventes.Pub=y

11. df

12. matplot(x, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

13. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Analyse:

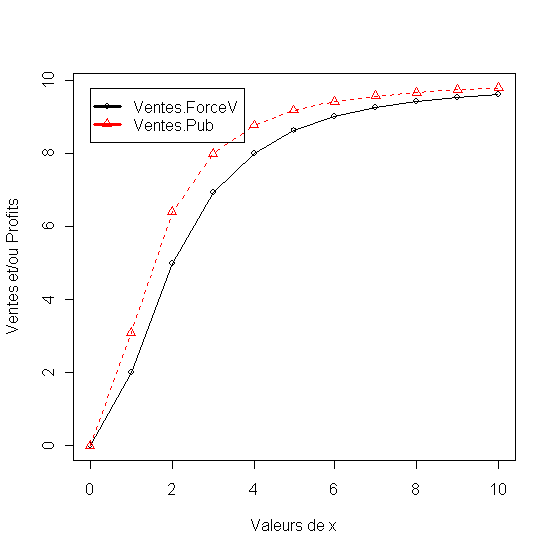
On utilise le modèle Adbudg lègèrement plus sensible grace au coefficient d=2 pour representer la réponse (Ventes.Pub) aux budget de publicité, et un modèle lègèrement moins sensible d=1.5 pour représenter la réaction (Ventes.ForceV) à taille de la force de ventes.

Figure 16 - Modèles Adbudg pour representer la sensibilité des ventes à la publicité et à la force de ventes.

Modèle à deux variables sans interactions [ 2.23]

Listing 14

1. a=10

2. b=0

3. c=2

4. d1=2

5. d2=1.5

6. x1<-seq(0,9,1) # varie

7. x2<-rep(0,10) # fix

8. g1<-b+(a-b)*((x1)^c/(d1^c+(x1)^c))

9. g2<-b+(a-b)*((x2)^c/(d2^c+(x2)^c))

10. y<-15+1*g1+1.6*g2

11. df<-data.frame(Effort=x1, Ventes.Pub=y)

12. x1<-rep(0,10) # fix

13. x2<-seq(0,9,1) # varie

14. g1<-b+(a-b)*((x1)^c/(d1^c+(x1)^c))

15. g2<-b+(a-b)*((x2)^c/(d2^c+(x2)^c))

16. y<-15+1*g1+1.6*g2

17. df$Ventes.ForceV=y

18. df

19. matplot(x2, df[,2:3], pch=1:2, type = "o", col = 1:2, xlab="Valeurs de x", ylab="Ventes et/ou Profits")

20. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Analyse:

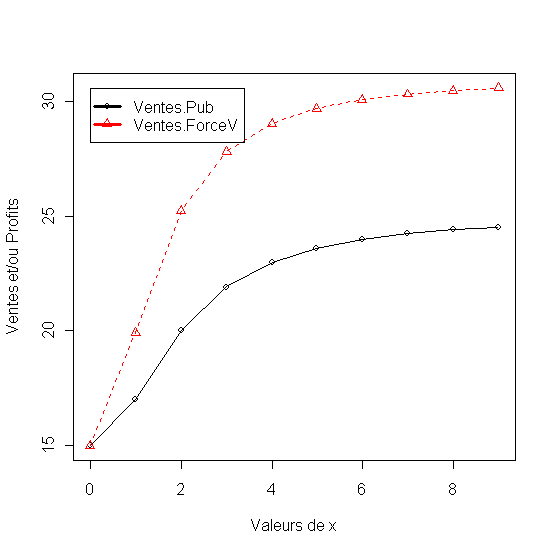
Malgrè le faite que le marché est légèrement plus sensible à la publicité, la force de vente est plus efficace avec un poids de 1.6 par rapport a seulment 1 pour la publicité dans le modèle qui regroupe les deux variables. Pour mettre en valeur cette différence d'efficacité on calcule deux cas de figure extrèmes. La premiere represente la réponse (Ventes.Pub) quand la taille de la force de ventes est réduite à zero et la publicité varie. La deuxieme represente la réponse (Vente.ForceV) quand la publicité est réduite à zéro et la taille de la force de vente varie.

Figure 17 - Modèle

Adjonction d'interaction

Q = ao + a1 g1 (X1) + a2 g2 (X2) + a3 g1 (X1) g2 (X2)

Exemples :

Modèle à deux variables avec interaction positive [ 2.24]
Modèle à deux variables avec interaction negative [ 2.25]

Listing 15

1. a=10

2. b=0

3. c=2

4. d1=2

5. d2=1.5

6. x1<-seq(0,9,1) # publicite varie

7. x2<-rep(5,10) # force de vent fixé a 5

8. g1<-b+(a-b)*((x1)^c/(d1^c+(x1)^c))

9. g2<-b+(a-b)*((x2)^c/(d2^c+(x2)^c))

10. y<-15+1*g1+1.6*g2

11. df<-data.frame(Effort=x1, Ventes.Interaction0 = y)

12. y<-15+1*g1+1.6*g2+0.05*g1*g2

13. df$Ventes.Interact.Pos = y

14. y<-15+1*g1+1.6*g2-0.05*g1*g2

15. df$Ventes.Interact.Neg = y

16. df

17. matplot(x1, df[,2:4], pch=1:4, type = "o", col = 1:3, xlab="Valeurs de x", ylab="Ventes et/ou Profits"

18. legend(min(x), max(df[,2:4]),names(df)[2:4], lwd=3, col=1:3, pch=1:3)

Analyse:

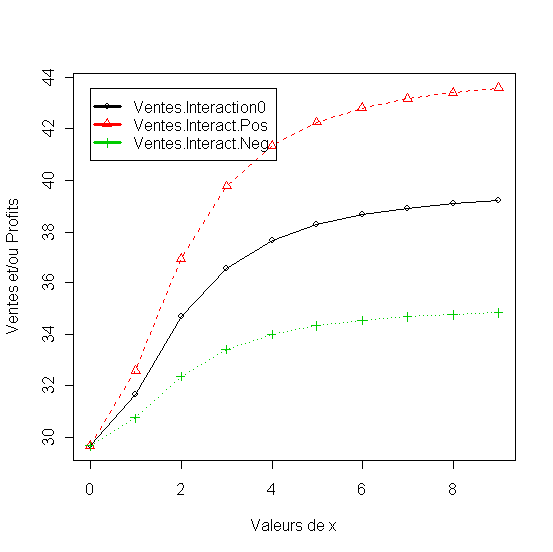
Pour illustrer les effets d'interaction entre les variables du mix marketing le modèle précedent est repris en utilisant un budget de publicité qui varie et un taille de la force de vente fixé à 5. Trois cas de figure sont présentés: le premièr sans interaction entre les deux variables, le deuxième avec un interaction positive et le dernier avec un interaction negative

Figure 18 - Effet d'interaction zero, positive et negative entre deux variable du mix marketing

Modèles multiplicatifs

modèle Log-Linéaire

Q = ao

on peut montrer que a1, a2 .. an sont des coefficients d'élasticité

Exemples :

Modèle loglinéaire recherche du prix optimum en gardant la pub. Fixé à 2 [ 2.30]
Modèle loglinéaire recherche du prix optimum en gardant la pub. Fixé à 8 [ 2.30_2]

Listing 16

1. x1<-rep(2,10)

2. x2<-seq(3,12,1)

3. y<-100*((+1*x1))^0.5*((+1*x2))^-2

4. profit<-(x2-3)*y-x1

5. df<-data.frame(Effort=x2, Profit2=profit)

6. x1<-rep(8,10)

7. y<-100*((+1*x1))^0.5*((+1*x2))^-2

8. profit<-(x2-3)*y-x1

9. df$Profit8=profit

10. df

11. matplot(x2, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

12. legend(min(x2), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Analyse:

En utilisant un modèle de réponse loglinéaire on cherche le prix (x2) optimum en fixant le budget de publicité (x1) dans un première étape à 2 et on calcul le profit (Profit2), ensuite on fait le même calcul avec le budget de pub. fixé à 8 pour obtenir une autre courbe du profit (Profit8).

Figure 19 - Le profit par rapport aux prix et deux niveaux de budget de publicité

Le prix optimum est proche de 6.

Modèle loglinéaire recherche du niveau de pub optimum avec le prix fixé à son optimum [ 2.30_3]
Modèle loglinéaire recherche du niveau de pub optimum avec le prix fixé au double de son optimum [ 2.30_4]

Listing 17

1. x1<-seq(0,45,1)

2. x2<-rep(6,46)

3. y<-100*((+1*x1))^0.5*((+1*x2))^-2

4. profit<-(x2-3)*y-x1

5. df<-data.frame(Effort=x1, Profit6=profit)

6. x2<-rep(12,46)

7. y<-100*((+1*x1))^0.5*((+1*x2))^-2

8. profit<-(x2-3)*y-x1

9. df$Profit12=profit

10. df

11. matplot(x1, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

12. legend(min(x1), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Analyse:

En posant le prix a sont niveau optimum determiné précédament (x2=6) on fait varier le budget du publicité pour obtenir une première courbe du profit (Profit6). Ensuite on double le prix (x2=12) et on applique la même variation de la publicité. Resulte une deuxième courbe du profit (Profit12)

Figure 20 - Le profit par rapport aux dépenses publicitaires et deux niveaux de prix

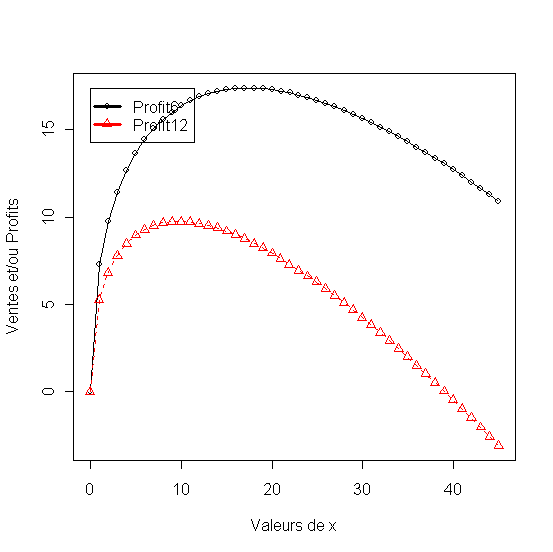
Modèles avec transformation logistique

Q =+ a2

Exemple :

Modèle d'interaction additif avec transformation logistique [ 2.34]

Q = + a2

Exemple

Modèle d'interaction multiplicatif avec transformation logistique [ 2.35]

Listing 18

1. x1<-seq(0,9,1)

2. x2<-rep(1,10)

3. y<-7/(1+exp(-(-3+x1+1.6*x2-0.05*x1*x2)))

4. df<-data.frame(Effort=x1, Ventes.Logit.Lin=y)

5. y<-7/(1+exp(-(x1^0.5*x2^-2)))

6. df$Ventes.Logit.Mult=y

7. df

8. matplot(x1, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

9. legend(min(x1), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Figure 21 - Transformation logistique des modèles d'interaction linéaires et multiplicatifs

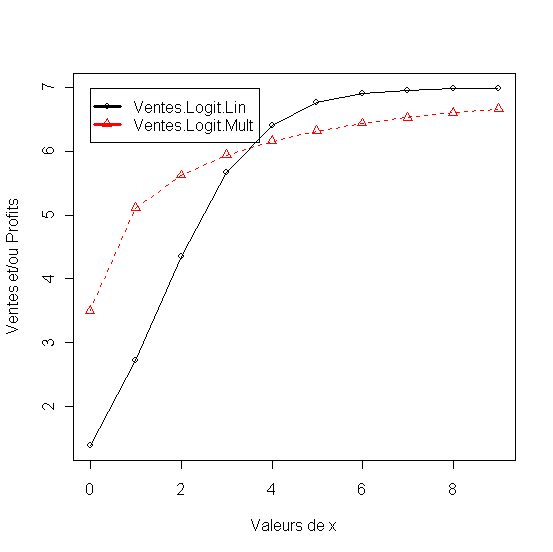
Modèles de part de marché

Modèles multiplicatifs

Si = ao

Modèles d'attractivité

notre part = nous/(nous + eux)

ou S = Q/(Q+V)

Si =

Ai = ao

ou i = 1 à I le nombre de marques sur le marché

Exemples

Analyses de sensibilité par rapport à « notre » publicité

Modèle de part de marché - Sensibilité à la Pulicité 1 [2.43-49.1]
Modèle de part de marché - Sensibilité à la Pulicité 2 [2.43-49.2]
Modèle de part de marché - Sensibilité à la Pulicité 3 [2.43-49.3]
Modèle de part de marché - Sensibilité à la Pulicité 4 [2.43-49.4]

Listing 19

1. # attribuer valeurs aux coefs

2. a1=2; b1=0.5; c1=2; d1=7

3. a2=0; b2=3; c2=-1.5; d2=0

4. a4=2; b4=0.5; c4=2 ; d4=7

5. a5=0; b5=3; c5=-1.5; d5=0

6. # Valeurs des variables marketing

7. x1<-seq(0,40,1) # notre pub

8. # Variables fixes

9. # Notre Prix; Leur pub ; Leur Prix

10. x2<-rep(2,41); x4<-rep(3,41) ; x5<-rep(2,41)

11. # Attractions

12. na<-1*(b1+(a1-b1)*((x1)^c1/(d1^c1+(x1)^c1)))^0.6*(a2+b2*(x2)^c2)^0.4

13. ca<-1*(b4+(a4-b4)*((+1*x4)^c4/(d4^c4+(+1*x4)^c4)))^0.6*(a5+b5*(x5)^c5)^0.4

14. # Part de marché

15. nms<-na/(na+ca)

16. df<-data.frame(Notre.Pub=x1, Part1=nms)

17. # Notre Prix; Leur pub ; Leur Prix

18. x4<-rep(6,41)

19. # Attractions

20. na<-1*(b1+(a1-b1)*((x1)^c1/(d1^c1+(x1)^c1)))^0.6*(a2+b2*(x2)^c2)^0.4

21. ca<-1*(b4+(a4-b4)*((+1*x4)^c4/(d4^c4+(+1*x4)^c4)))^0.6*(a5+b5*(x5)^c5)^0.4

22. # Part de marché

23. nms<-na/(na+ca)

24. df$Part2=nms

25. # Notre Prix; Leur pub ; Leur Prix

26. x4<-rep(3,41)

27. x5<-rep(1.6,41)

28. # Attractions

29. na<-1*(b1+(a1-b1)*((x1)^c1/(d1^c1+(x1)^c1)))^0.6*(a2+b2*(x2)^c2)^0.4

30. ca<-1*(b4+(a4-b4)*((+1*x4)^c4/(d4^c4+(+1*x4)^c4)))^0.6*(a5+b5*(x5)^c5)^0.4

31. # Part de marché

32. nms<-na/(na+ca)

33. df$Part3=nms

34. # Notre Prix; Leur pub ; Leur Prix

35. x2<-rep(1.6,41)

36. x5<-rep(2,41)

37. # Attractions

38. na<-1*(b1+(a1-b1)*((x1)^c1/(d1^c1+(x1)^c1)))^0.6*(a2+b2*(x2)^c2)^0.4

39. ca<-1*(b4+(a4-b4)*((+1*x4)^c4/(d4^c4+(+1*x4)^c4)))^0.6*(a5+b5*(x5)^c5)^0.4

40. # Part de marché

41. nms<-na/(na+ca)

42. df$Part4=nms

43. matplot(x1, df[,2:5], pch = 1:4, type = "o", col = 1:4,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

44. legend(min(x), max(df[,2:5]),names(df)[2:5], lwd=3, col=1:4, pch=1:4)

Figure 22 - Analyse de sensibilité de la part de marché aux dépenses publicitaire et aux actions de la concurence

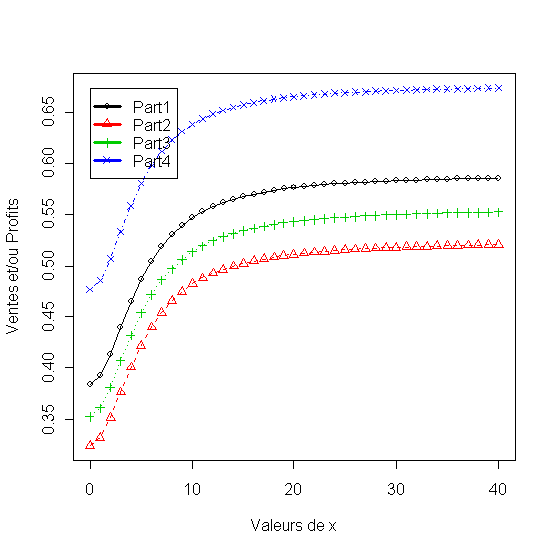
Analyses de sensibilité par rapport à « notre » prix

Modèle de part de marché - Sensibilité au Prix 5 [2.43-49.5]
Modèle de part de marché - Sensibilité au Prix 6 [2.43-49.6]
Modèle de part de marché - Sensibilité au Prix 7 [2.43-49.7]
Modèle de part de marché - Sensibilité au Prix 8 [2.43-49.8]

Listing 20

1. # attribuer valeurs aux coefs

2. a1=2; b1=0.5; c1=2; d1=7 # Pub Adbudg

3. a2=0; b2=3; c2=-1.5; d2=0 # Prix Fracroot

4. a4=2; b4=0.5; c4=2 ; d4=7 # Pub Adbudg

5. a5=0; b5=3; c5=-1.5; d5=0 # Prix Fracroot

6. # Valeurs des variables marketing

7. x2<-seq(1,6,1) # notre prix

8. # Variables fixes

9. # Notre Prix; Leur pub ; Leur Prix

10. x1<-rep(3,6)

11. x4<-rep(3,6)

12. x5<-rep(2,6)

13. # Attractions

14. na<-(b1+(a1-b1)*(x1^c1/(d1^c1+x1^c1)))^0.6*(a2+b2*x2^c2)^0.4

15. ca<-(b4+(a4-b4)*(x4^c4/(d4^c4+x4^c4)))^0.6*(a5+b5*x5^c5)^0.4

16. # Part de marché

17. nms<-na/(na+ca)

18. df<-data.frame(Notre.Pub=x1, Part1=nms)

19. # Notre Pub

20. x1<-rep(6,6)

21. # Attractions

22. na<-(b1+(a1-b1)*(x1^c1/(d1^c1+x1^c1)))^0.6*(a2+b2*x2^c2)^0.4

23. ca<-(b4+(a4-b4)*(x4^c4/(d4^c4+x4^c4)))^0.6*(a5+b5*x5^c5)^0.4

24. # Part de marché

25. nms<-na/(na+ca)

26. df$Part2=nms

27. x1<-rep(3,6)

28. x4<-rep(6,6)

29. # Attractions

30. na<-(b1+(a1-b1)*(x1^c1/(d1^c1+x1^c1)))^0.6*(a2+b2*x2^c2)^0.4

31. ca<-(b4+(a4-b4)*(x4^c4/(d4^c4+x4^c4)))^0.6*(a5+b5*x5^c5)^0.4

32. # Part de marché

33. nms<-na/(na+ca)

34. df$Part3=nms

35. # Notre Prix; Leur pub ; Leur Prix

36. x4<-rep(3,6)

37. x5<-rep(1.6,6)

38. # Attractions

39. na<-(b1+(a1-b1)*(x1^c1/(d1^c1+x1^c1)))^0.6*(a2+b2*x2^c2)^0.4

40. ca<-(b4+(a4-b4)*(x4^c4/(d4^c4+x4^c4)))^0.6*(a5+b5*x5^c5)^0.4

41. # Part de marché

42. nms<-na/(na+ca)

43. df$Part4=nms

44. matplot(x2, df[,2:5], pch = 1:4, type = "o", col = 1:4,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

45. legend(min(x2), max(df[,2:5]),names(df)[2:5], lwd=3, col=1:4, pch=1:4)

Figure 23 - Sensibilité de la part de marché aux prix et aux actions de la concurence

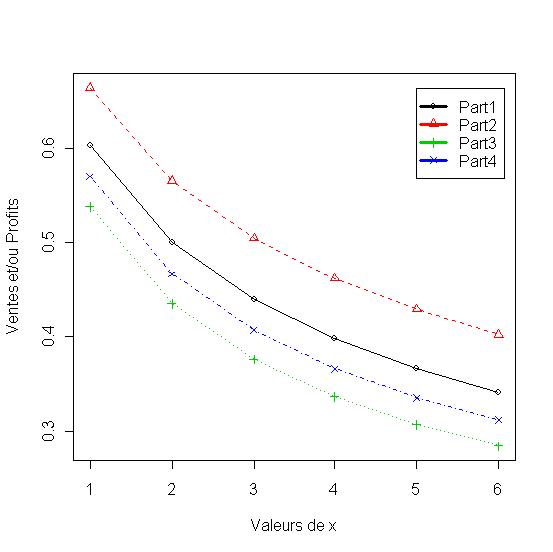
Recherche du budget de publicité qui assure un profit optimum quand notre prix et celui de la concurence = 2 et la publicité du concurent = 2.

Figure 24 - Analyse de sensibilité de publicité

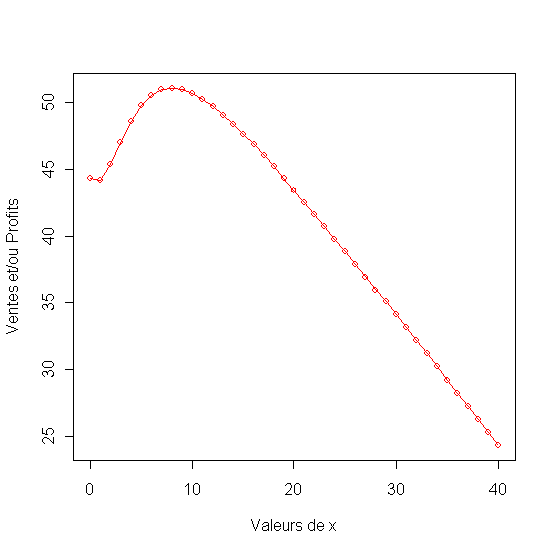
Sensibilité du profit par rapport au prix quand la publicité = 7 elle met en evidence un prix optimal de 4.5.

Figure 25 - Sensibilité du profit par rapport au prix

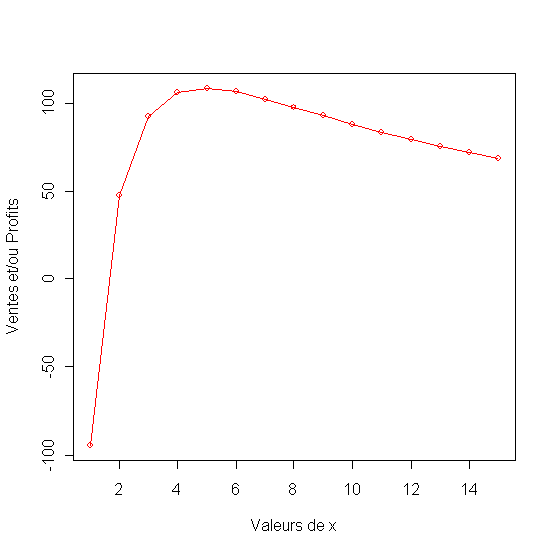
Depenses publicitaires optimales quand on applique le prix optimal (4.5)

Figure 26 - Dépenses publicitaire optimales en utilisant le prix optimum déterminé auparavant

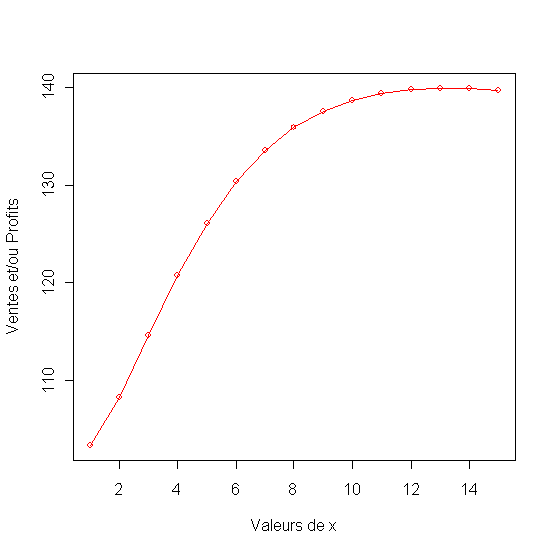
Figure 27

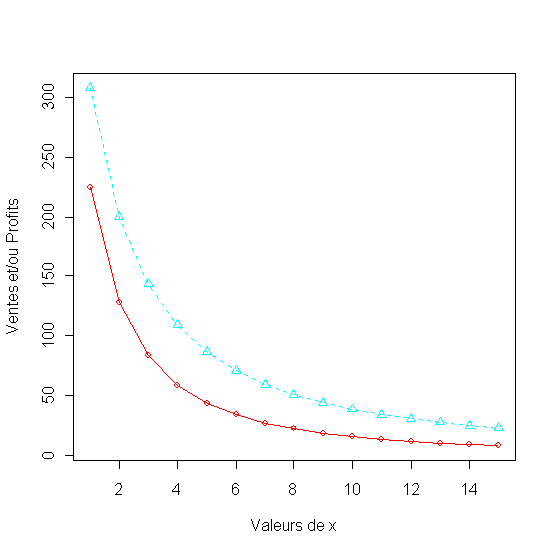
Nos ventes comparées aux ventes totales du marché à différents niveau de prix. On observe que pour le prix optimum (x2=4.5) et quand on utilise le budget de publicité optimum (x1=7) notre part de marché sera de 55%.

Interaction Competitive Multiplicative (MCI)

Ai =ei

la forme linéarisé du modèle de part de marché (Si) est:

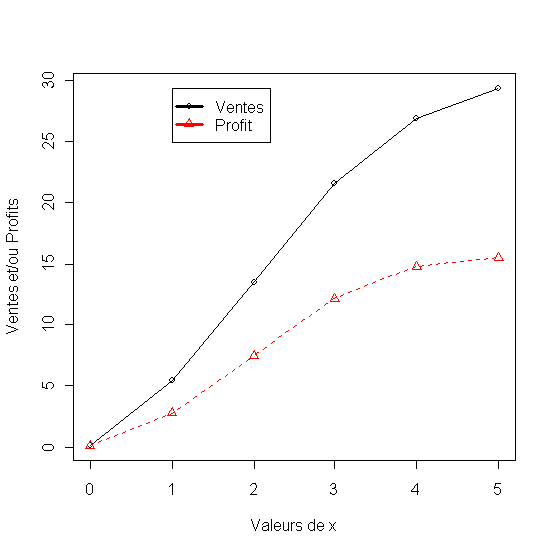
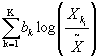log= ai* ++ ei*

ou , , sont les moyennes géométriques de Si,et ei et

ai* = ai -

ei* = log (ei /i)

Example [2.50.1]

Logit Multinomial (MNL)

Ai = exp(ai+ + ei)

la forme linéarisée du modèle de part de marché (Si) est:

log= ai* +#+ (ei-)

Effets dynamiques

Lissage exponentiel et prcédure de Koyck

Q_t = a₁ f (X_t) + a₂ f (X_t-1) + a₃ f (X_t-2) + ...

on suppose que l'effet de X sur Q décroît de manière régulière ( = l ) et on transforme la formule:

Qt = a₁ f (X_t) + a₁λ f (X_t-1) + a₁ λ ² f (X_t-2) + ...

On utilise la procédure de Koyck:

1) on décale l'équation précédente d'une période et on la multiplie avec λ :

λ Q_t-1 = λ a₁ f (X_t-1) + λ ²a₁ f (X_t-2) + ...

2) et on soustrait les deux équations

Q_t - λ Q_t-1 = a₁ f (X_t)

a₁ mesure l'effet à court terme et l l'effet des actions passées

quand pendant des longues périodes le Ventes et la publicité sont stables (Xt = Xt-1 et Qt = Qt-1 = Q) la dernière équation devient:

Q =f (X)

ou mesure l'effet à long terme de l'effort marketing et est le terme multiplicative des dépenses marketing sur le long terme.

Exemples

On utilise les modèle d'efficacité des dépenses publicitaires 2.30 et 2.31 (publicité statique optimum est 10 et prix statique optimal = 6

Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,2) dépense constante[2.59.1]
Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,2) dépenses par impulsions [2.59.2]
Effets dynamiques des dépenses publicitaires, fort effet dynamique (0,8) dépense constante[2.59.3]
Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,8) dépenses par impulsions [2.59.4]
Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,8) dépense constante sous contrainte budgetaire[2.59.5]
Effets dynamiques des dépenses publicitaires, faible effet dynamique (0,8) dépenses par impulsions sous contrainte budgetaire[2.59.6]

Listing 21

1. x2=rep(6,10)

2. x1=rep(15,10)

3. alfa=0.8

4. lambda=0.2

5. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2

6. y<-rep(0,10)

7. y[1]<-ylong[1]

8. for(i in 2:10){

9. y[i]<-alfa*ylong[i]+lambda*y[i-1]

10. }

11. profit<-(x2-1.5)*y-x1

12. df<-data.frame(Ventes=y, Profit1=profit)

13. x1=rep(c(25,5),5)

14. alfa=0.8

15. lambda=0.2

16. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2

17. y<-rep(0,10)

18. y[1]<-ylong[1]

19. for(i in 2:10){

20. y[i]<-alfa*ylong[i]+lambda*y[i-1]

21. }

22. profit<-(x2-1.5)*y-x1

23. df$Profit2=profit

24. x1=rep(15,10)

25. alfa=0.2

26. lambda=0.8

27. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2

28. y<-rep(0,10)

29. y[1]<-ylong[1]

30. for(i in 2:10){

31. y[i]<-alfa*ylong[i]+lambda*y[i-1]

32. }

33. profit<-(x2-1.5)*y-x1

34. df$Profit3=profit

35. x1=rep(c(25,5),5)

36. alfa=0.2

37. lambda=0.8

38. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2

39. y<-rep(0,10)

40. y[1]<-ylong[1]

41. for(i in 2:10){

42. y[i]<-alfa*ylong[i]+lambda*y[i-1]

43. }

44. profit<-(x2-1.5)*y-x1

45. df$Profit4=profit

46. x1=rep(5,10)

47. alfa=0.2

48. lambda=0.8

49. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2

50. y<-rep(0,10)

51. y[1]<-ylong[1]

52. for(i in 2:10){

53. y[i]<-alfa*ylong[i]+lambda*y[i-1]

54. }

55. profit<-(x2-1.5)*y-x1

56. df$Profit5=profit

57. x1=rep(c(9,1),5)

58. alfa=0.2

59. lambda=0.8

60. ylong<-100*((+1*x1))^0.5*((+1*x2))^-2

61. y<-rep(0,10)

62. y[1]<-ylong[1]

63. for(i in 2:10){

64. y[i]<-alfa*ylong[i]+lambda*y[i-1]

65. }

66. profit<-(x2-1.5)*y-x1

67. df$Profit6=profit

68. df

69. matplot(1:10, df[,2:7], pch = 1:6, type = "o", col = 1:6,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

70. legend(1, max(df[,2:7]),names(df)[2:7], lwd=3, col=1:6, pch=1:6)

Figure 28 - Depenses publicitaires constantes ou par impulsion et effets dynamiques

Modèle de Bass ou modèle de diffusion des nouveaux produit

Le modèle de Bass postule que le taux d'adoption d'un nouveau produit dépend à chaque période du nombre de clients potentiels n'ayant pas encore adopté le produit pondéré par un facteur externe qui exprime par exemple l'effet de la publicité et d'un effet de bouche à oreille qui lui dépend du nombre de nouveaux adopteurs de la période précédente pondéré par un facteur externe qui contrôle l'importance de cet effet.

y_t<-(a+b*y_t-1 )(N-ycum_t-1)

ou a= facteur externe, b= facteur interne, N= nombre de clients potentiel, ycum = Sy

Exemple

Le potentiel du marché est fixé à 1000, la durée du processus analysé est de 20 périodes le facteur externe (effet de publicité) a=0,01 et le facteur interne (importance du bouche à oreille) b=0,001. [2.65]

Listing 22

1. a=0.01 # external factor

2. b=0.001 # internal factor

3. ycum=0

4. y<-rep(0,20)

5. for(i in 2:20){

6. y[i]<-(a+b*y[i-1])*(1000-ycum)

7. ycum=ycum+y[i]

8. }

9. y

10. matplot(1:20, y, pch = 1:1, type = "o", col = 1:1,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

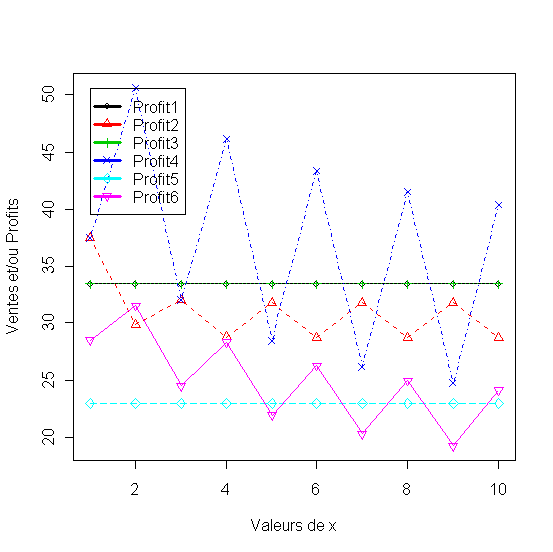
Analyse

Les premières quatre lignes de code donnent des valeurs aux variables a, b et initialisent la variable ycum et le vecteur y à zéro.

Les lignes 5 et 8 renferment une boucle ou i progresse de 2 à 20. Pour chaque i à la ligne 6 la i^ème valeur du vecteur y est le produit de 1000 moins ycum et d'une fonction linéaire de sa valeur précédente y[i-1]. ycum est la somme cumulée durant i étapes du vecteur y. La ligne 9 affiche les valeurs du vecteur y à la fin du processus (boucle) et la ligne dix représente graphiquement les valeurs de y qui correspondent à chaque période.

La relation dans la boucle veut dire que y[i] le nombre d'adopteurs du nouveau produit à la période i dépend du nombre de nombre de clients potentiels n'ayant pas encore adopté le produit (1000-ycum) pondéré par un facteur externe comme l'effet de la publicité (a) et un effet de bouche à oreille qui lui dépend des nouveaux adopteurs de la période précédente y[i-1] multiplié par le facteur interne (b).

Figure 29 - Les cycle e vie d'un produit exprimé en terme de ventes (modèle de diffusion de Bass)

Modèles de réaction au mix marketing

Presentation

Les sections suivantes s'organisent autour de la notion de mix marketing et focalisent sur chacune des variables qui composent le mix marketing et présente des modèles qui représentent l'impact de chaque variable, c'est à dire:

Modèles de choix de produits
Modèles de prix
Modèles publicitaires
Modèles de Promotion de ventes
Modèles de la Force de ventes

Modèles de choix des caractéristiques des produits

Presentation

On s'intéresse ici aux caractéristiques qui affectent le positionnement perçu des produits. Les limites cognitives de l'homme font qu'en générale

Modèles de la Valeur Espérée

fondées sur le principe d'accumulation, où "l'utilité" totale est la somme des niveaux de perception () de l'objet sur chacun des critères, pondérée par l'importance () associée à ce niveau de perception par l'interviewé:

pi =

où pi est l'utilité associé au produit par l'individu i

Si p_i est la probabilité d'acheter le produit de l'individu i, alors la demande du marché est la somme de ces probabilités

Observations : p_i sont inconues d'avance et le W_ik et X_ik sont des mesures declaratives ..

Exemple

Politique de produit - Modèles de valeur espérée [ 4.1-3]

Listing 23

1. # Modèles de valeur espérée

2. K=2 # no critères

3. I=10 # no individus

4. # Perception produit echelle 1-7

5. # input (1)

6. x<-round(runif(I*K, min=1, max=7))

7. dim(x)<-c(I,K)

8. colnames(x)<-colnames(x, do.NULL=F, prefix="Percp.")

9. # Importance des critères par individu

10. # input (2)

11. w<-round(runif(I*K, min=1, max=5))

12. dim(w)<-c(I,K)

13. colnames(w)<-colnames(w, do.NULL=F, prefix="Import.")

14. # Scores Individuels proportionnels aux probabilités dachat

15. p<-(x*w)%*%c(1,1)

16. dim(p)<-c(I,1)

17. maxp=max(p)

18. maxprob=0.3

19. p<-maxprob*p/maxp

20. colnames(p)<-"Prob.achat"

21. rownames(p)<-rownames(p, do.NULL=F, prefix="Obs.")

22. df<-data.frame(cbind(p,x,w))

23. df

24. cat("Ventes")

25. (sum(df[,"Prob.achat"]))

26. # Effets de la modification des caractéristiques dun produit

27. # input (3)

28. deltax=c(0,2)

29. deltaVentes=sum(((w%*%diag(deltax))%*%c(1,1))%*%(maxprob/maxp))

Régression de la Préférence

p_i =

p_i = le jugement de préférence du produit pour l'individu i (peut être un score où un classement de préférence)

W_k = importance à estimer par le modèle de la caractéristique Xki.

= évaluation par l'individu i du produit suivant la caractéristique k.

Observations

Exemple

Politique de produit - Regression de la préférence[4.4]

Listing 24

1. # Regression de la preférence

2. K=2 # no critères

3. I=10 # no produits

4. # Perception produit echelle 1-7

5. # input (1)

6. x<-round(runif(I*K, min=1, max=7))

7. dim(x)<-c(I,K)

8. colnames(x)<-colnames(x, do.NULL=F, prefix="Percp.")

9. # Score de préférence

10. # importance à estimer de critères pour un groupe dindividus

11. # input (2)

12. w<-c(0.3, 0.7)

13. err<-rnorm(10,1, 0.5)

14. p<-round(x%*%(w)+err)

15. colnames(p)<-"ScorePref"

16. rownames(p)<-rownames(p, do.NULL=F, prefix="Obs.")

17. df<-data.frame(cbind(p,x))

18. df

19. # Estimation de limportance acordée aux caractéristique par un même groupe dindividu

20. w.lm<-lm(p~0+x)

21. w.lm[[1]]

Tableau 6 - Scores de préférences et perceptions des caracteristique d'un produit

       ScorePref Percp.1 Percp.2

Obs.1          6       3       7

Obs.2          4       4       3

Obs.3          8       5       6

Obs.4          5       1       6

Obs.5          6       3       5

Obs.6          7       4       5

Obs.7          6       2       7

Obs.8          7       4       7

Obs.9          5       2       5

Obs.10         3       1       2

Estimation par regression de limportance acordée aux caractéristique par un même groupe d'individus

Tableau 7 - Coefficient d'importance estimés par regression

   xPercp.1  xPercp.2

0.7023002 0.6776436

L'Analyse Conjointe

pim =

ou pim = est la préférence de l'individu i pour le produit m (exprimé sous forme d'un classement ou scores)

l imk = utilité partielle de l'individu i estimé pour le produit m sur la caractéristique k

dmkp = variable muette indiquant la présence (d=1) ou l'absence (d=0) du niveau p de la caractéristique k dans le produit m

Exemple :

Politique de produit - Analyse conjointe [4.5]

Listing 25

1. # Plan dexperience complet des niveaux dattributs

2. dd <- data.frame(a = gl(2,12), b = gl(4,3,24), c=gl(3,1,24)) # balanced 3-way

3. dd

4. # Modèle de préférence individuelle

5. mm<-model.matrix(~ 0+ a + b + c, dd)

6. pref<-order(runif(24))

7. df<-data.frame(cbind(pref,mm))

8. colnames(df)<-c("ordre", "a1", "a2", "b2", "b3", "b4", "c2", "c3")

9. df

10. #Utilités partielles

11. attach(df)

12. conj.lm<-lm(df$ordre~ 0 + df$a1+ df$a2 + df$b2 + df$b3 + df$b4 + df$c2 + df$c3)

13. conj.lm[[1]]

Tableau 8 - Analyse conjointe sur 24 concepts de produits

Plan d'expériences complet

Ordre de preference en fonction des niveaux des attributs

  a b c

1 1 1 1

2 1 1 2

3 1 1 3

4 1 2 1

5 1 2 2

6 1 2 3

7 1 3 1

8 1 3 2

9 1 3 3

10 1 4 1

11 1 4 2

12 1 4 3

13 2 1 1

14 2 1 2

15 2 1 3

16 2 2 1

17 2 2 2

18 2 2 3

19 2 3 1

20 2 3 2

21 2 3 3

22 2 4 1

23 2 4 2

24 2 4 3

  ordre a1 a2 b2 b3 b4 c2 c3

1   17 1 0 0 0 0 0 0

2   4 1 0 0 0 0 1 0

3   21 1 0 0 0 0 0 1

4   22 1 0 1 0 0 0 0

5   1 1 0 1 0 0 1 0

6   14 1 0 1 0 0 0 1

7   6 1 0 0 1 0 0 0

8   24 1 0 0 1 0 1 0

9   2 1 0 0 1 0 0 1

10  16 1 0 0 0 1 0 0

11  18 1 0 0 0 1 1 0

12   5 1 0 0 0 1 0 1

13  10 0 1 0 0 0 0 0

14   3 0 1 0 0 0 1 0

15  12 0 1 0 0 0 0 1

16  20 0 1 1 0 0 0 0

17  23 0 1 1 0 0 1 0

18  15 0 1 1 0 0 0 1

19   7 0 1 0 1 0 0 0

20  13 0 1 0 1 0 1 0

21   8 0 1 0 1 0 0 1

22  19 0 1 0 0 1 0 0

23   9 0 1 0 0 1 1 0

24  11 0 1 0 0 1 0 1

Estimation (ici par regression linéaire) des utilités partielle accordées par l'individu (client) aux différents niveaux d'attributs

Tableau 9 - Utilités partielles estimées (ici par regression) des niveaux d'attributs

    df$a1     df$a2     df$b2     df$b3     df$b4     df$c2     df$c3

13.291667 13.291667  4.666667 -1.166667  1.833333 -2.750000 -3.625000

Autre exemples

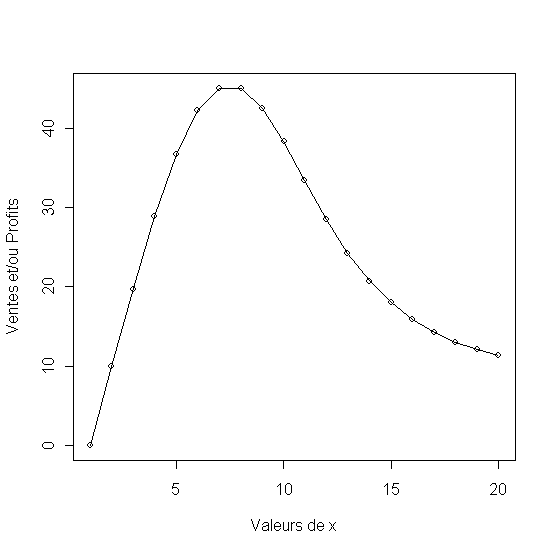
Politique de produit - Ventes espérées suivant la durée de la garantie[4.6]

Listing 26

1. a=35

2. b=-2

3. c=1

4. d=-4

5. x<-seq(0,5,1)

6. y<-a*(1/(1+exp(-b-c*(x))))+d

7. profit<-0.7*y-x

8. df=data.frame(PerGarantie=x, Ventes=y, Profit=profit)

9. df

10. matplot(x, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

11. legend(1, max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Figure 30 - Ventes espérées en fonction de la durée de la période de garantie

Modèles de Prix

Le modèle Classique

Fonction linéaire

Q = a - bP

Fonction de Demande à élasticité constante de Prix

Q = aPb

Exemples

Modèle de demande linéaire par rapport au prix[4.10-11]

Listing 27

1. x<-seq(0,10,1)

2. y<-+30-4*x

3. profit<-y*(x-1.5)

4. df<-data.frame(Effort=x, Ventes=y, Profit=profit)

5. df

6. matplot(x, df[,2:3], pch = 1:2, type = "o", col = rainbow(2),xlab="Valeurs de x", ylab="Ventes et/ou Profits")

Figure 31 - Ventes et profit avec une fonction de demande linéaire

Modèle de demande à élasticité de prix constante[4.13-14]

Listing 28

1. x<-seq(1,10,1)

2. y<-90*(x)^-1.5

3. profit<-y*(x-1.5)

4. df<-data.frame(Effort=x, Ventes=y, Profit=profit)

5. df

6. matplot(x, df, pch = 1:2, type = "o", col = rainbow(2),xlab="Valeurs de x", ylab="Ventes et/ou Profit")

7. legend(1, max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Figure 32 - Vente et profit avec une fonction de demande à élasticité constante

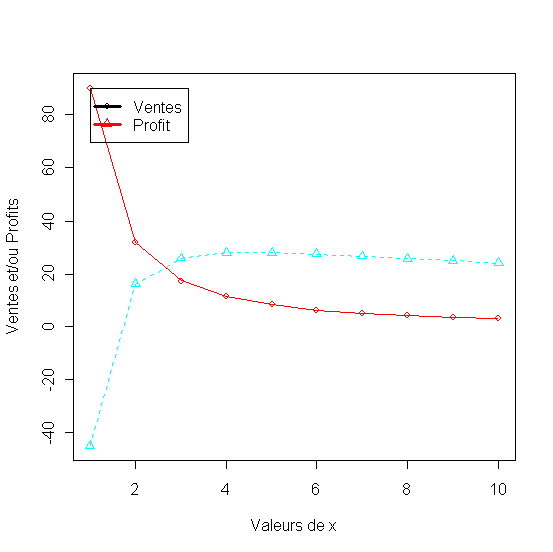
Le prix psychologique

Gabor et Granger (1966) et Sowter, Gabor et Granger (1971) caractérisent le rapport entre le prix et la qualité par le concept de limite - une relation connue en littérature économique comme le prix de réservation.

Un consommateur ayant l'intention d'acheter le produit à deux limites des prix à l'esprit: une limite supérieur au-dessus de la quelles il trouvera le produit trop cher et une limite inférieure en-dessous de la quelle il doute de la qualité du produit.

Fixation du prix - Etat des connaissances

Lilien et Kotler affirment que les sociétés n'excellent pas dans la détermination du prix optimal. Elle ne tiennent pas suffisamment compte de l'intensité de la demande et de la psychologie du client. Les prix sont fixé souvent indépendamment de la stratégie de positionnement. Il ne varient suffisamment pour qu'on puisse enregistrer les différences de réaction en fonction de articles et des segments de marché.

Les modèles de prix sont en général statique et ne permettent pas d'identifier des changements du marché.

Exemple

Méthode du prix psychologique [ p.81]

Listing 29

1. # Prix psychologique

2. ptropbas<-pnorm(30:130,60,15)

3. ptropcher<-pnorm(30:130, 100,15)

4. prixopt<-(ptropbas-ptropcher)

5. df<-data.frame(TropBas=ptropbas, Optimum=prixopt, TropCher=ptropcher)

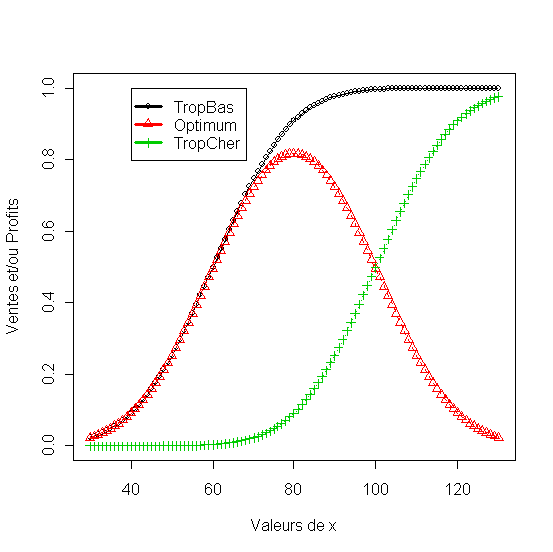
6. matplot(30:130, df, pch = 1:3, type = "o", col = 1:3,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

7. legend(40, max(df),names(df), lwd=3, col=1:2, pch=1:3)

Figure 33 - Méthode du prix psychologique

Prise en compte de la courbe d'expérience

C(t) = k V(t)-b

ou C(t) est le coût unitaire de production; V(t) est le volume de production cumulée, k et b sont des constantes

Exemple: les modèle utilisés par Dolan et Jeuland (1981), pour étudier la fixation des prix dans un marché monopolistique avec une baisse de coût lié à la courbe d'expérience et plusieurs fonctions de demande dont:

V(t) = a e -dP(t)

concrètement on peut analyser la rentabilité relative de trois politiques de prix différentes (hausse des prix, prix constants, baisse des prix) pendant plusieurs périodes utilisant les expressions suivantes:

V(t) = 150 e -0,3 Prix(t)

C(t) = 10 V(t-1)-0,2

Exemple :

Fixation du prix au cours du temps avec baisse du coût lié à la courbe d'expérience [4.15-16]

Listing 30

1. # Fixation du prix au cours du temps avec baisse du coût lié à la courbe dexpérience

2. t<-0:8

3. print("Prix décroissant")

4. prix<-seq(7,3,-0.5)

5. #cat("Prix constant")

6. #prix<-rep(5,10)

7. #cat("Prix croissant")

8. #prix<-seq(3,7,0.5)

9. # Ventes en fonction du prix(t)

10. ventes<-150*exp(-0.3*prix)

11. # Ventes cumulées

12. ventescum<-rep(0,9)

13. ventescum[1]=ventes[1]

14. for(i in 2:9)

15. ventescum[i]=ventescum[i-1]+ventes[i]

16. cout<-10*ventescum^-0.2

17. df<-data.frame(Prix=prix, Ventes=ventes, VentesCum = ventescum, Cout=cout)

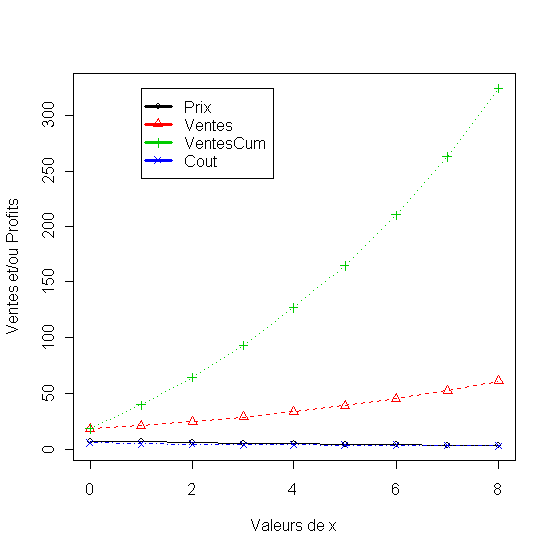
18. matplot(t, df, pch = 1:4, type = "o", col = 1:4,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

19. legend(1, max(df),names(df), lwd=3, col=1:4, pch=1:4)

Figure 34 - Fixation du prix en fonction de la courbe d'experience

Modèles Publicitaires

Un modèle de réaction à la publicité

Le modèle BRANDAID (Little, 1975) dans sa partie destinée à la publicité par d'un niveau de ventes de référence Vo et postule qu'il existe un taux de publicité po (taux de référence) qui maintiendra ce niveau de ventes. Il suppose aussi que les réaction à long terme vers r(a) des ventes à un certain taux de publicité (index) a(t) = p(t)/po (ou p(t) est le taux de publicité au temps t il est fonction du budget publicitaire, l'efficacité média et du rendement de la création publicitaire) tende des valeurs asymptotiques données par l'expression:

r[a(t)] = k (1- e-b a(t)) + c

La dynamique du processus est donnée par les expressions suivantes:

e(t) = a e(t-1) + (1-a ) r[a(t)]

V(t) = Vo e(t)

ou V(t) sont les ventes à l'instant t

pour intégrer l'effet de la mémorisation sur l'index publicitaire a on peut redéfinir a(t)

a'(t) = b a'(t-1) + (1-b ) a(t)

Exemple pour le tableur:

r[a(t)] = 2,5 [1 - e-0,25 a(t)] + 0,45

Exemples

Modèle pblicitaire - Stratégie de publicité constante [ 4.17-21.1]
Modèle pblicitaire - Stratégie de publicité par impulsions [ 4.17-21.2]

Les deux modèles font jouer les effets dynamique (effet imediat lambda et effet à long terme terme alfa). Les deux stratégies sont: Stratégie 1 (pub const.) 1,2 par période; Stratégie 2 (pub par impulsions) dépenses de pub alternavites: 1,4; 1; 0; ...

Listing 31

1. # Effets dynamiques

2. alpha1=0.8

3. lambda=0.2

4. # Modèle pblicitaire 1

5. print("Stratégie de publicité constante")

6. at<-rep(1.2,10) # pub constante

7. rat<-2.5*(1-exp(-0.25*at))+0.45 # réaction à long terme des ventes à la pub (index)

8. S0=100 # Ventes initiales

9. et=rep(1,10)

10. for(i in 2:10)

11. et[i]=alpha1*et[i-1]+lambda*rat[i] # indice d`effet de la publicité

12. St=S0*et # Ventes par periode

13. df<-data.frame(Temps=1:10, Ventes=St)

14. # Modèle pblicitaire 2

15. print("Stratégie de publicité par impulsions")

16. at<-rep(c(1.4,1),5) # pub par impulsions

17. rat<-2.5*(1-exp(-0.25*at))+0.45 # réaction à long terme des ventes à la pub (index)

18. S0=100 # Ventes initiales

19. et=rep(1,10)

20. for(i in 2:10)

21. et[i]=alpha1*et[i-1]+lambda*rat[i] # indice d`effet de la publicité

22. St=S0*et # Ventes par periode

23. df$Ventes2=St

24. df

25. matplot(df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

26. legend(1, max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Figure 35 - Comparaison de l'efficacité des politique de dépenses publicitaires: constantes et par impulsions

La Réaction à la Publicité - Etat des connaissances

Il existe un grand nombre de modèles. La plupart sont linéaires ou multiplicatifs avec des effets dynamiques estimés avec des données empiriques. Il y à aussi des formes complexes de modèles paramètres par des estimations subjectives.

Les Modèles de Promotion des Ventes

Un modèles promotionnel

La Réaction à la promotion - Etat des connaissances

Les Modèles de la Force de Vente

Pratique de la Fixation de la Taille de la Force de Vente

Les Méthodes d'Analyse de la Réaction du Marché

La Réaction des Ventes à la Force de Vente - Etat des Connaissances
Exemples

Modèle Promotionel - variation de ventes avec la part de marché [ 4.22-25.1]

Listing 32

1. x1<-seq(0,0.9,0.1) # parts de marché de la marque (varie)

2. x2<-rep(3,10) # cout de la promotion ( valeur fixe)

3. f1<-20*x1^0.3*(1-x1) # volume du marché * impact * potentiel

4. f2<-x2^2/(3^2+x2^2) # effet de l`ampleur de la promotion

5. y<-f1*f2 # volume * impact * potentiel * ampleur

6. profit<-y-x2

7. df<-data.frame(PartM=x1, Ventes=y, Profit=profit)

8. df

9. matplot(x1, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

10. legend(min(x1), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

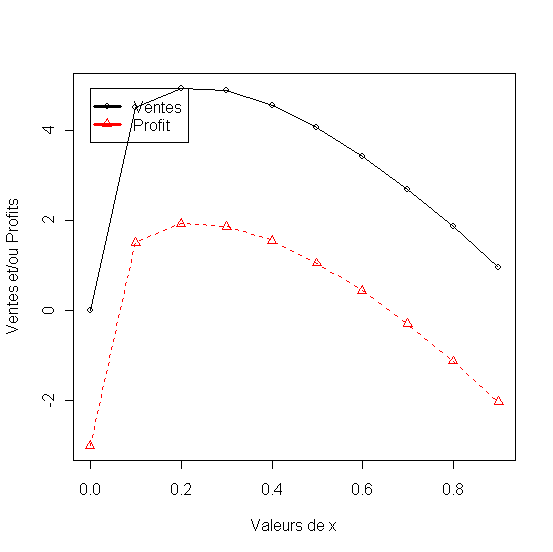
L'effet sur les ventes dépend du volume du marché (ici 20), de l'impacte de la promotion (une mesure d'accessibilité à la promotion pour ce qui ne benefient pas directment - ici x1^0.3) , le potentiel ou la fraction du marché qui n'est pas touché par la mesure à l'instant present - ici (1-x1) et l'ampleur de la promotion (ou la mesure dans laquelle l'importance de la promotion arrive à tenter l'individu, en general un courbe en "S" en fonction de la valeur de la promotion - ici une fonction ADBUDG) .

Figure 36 - Ventes et profit en fonction de la part de marché initiale de la marque promue

Modèle Promotionel - niveau de la promotion optimum pour un part de marché donnée [ 4.22-25.2]

Listing 33

1. x1<-rep(0.1,10) # parts de marché de la marque

2. x2<-0:9 # cout de la promotion

3. f1<-20*x1^0.3*(1-x1) # impact * potentiel

4. f2<-x2^2/(3^2+x2^2) # effet de l`ampleur de la promotion

5. y<-f1*f2

6. profit<-y-x2

7. df<-data.frame(Promotion=x2, Ventes=y, Profit=profit)

8. df

9. matplot(x2, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

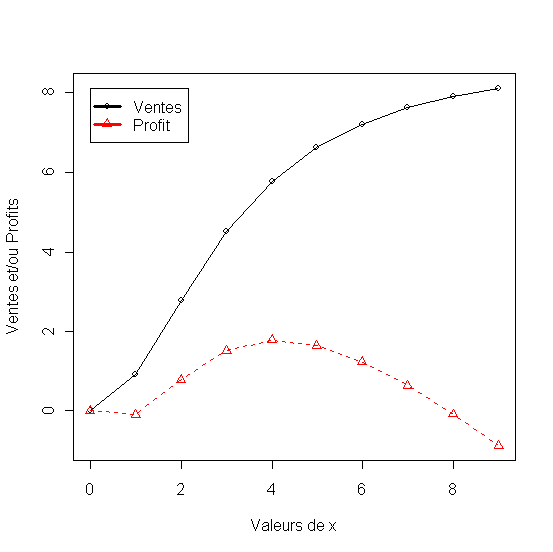
10. legend(min(x2), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

Figure 37 - Analyse de sensibilité des Ventes et du Profit avec un part de marché initiale de 10%

Les Modèles de la Force de Vente

Exemples :

Modèle de la Force de vente [ 4.27-29]

Listing 34

1. # Modèle de la Force de vente

2. # d`après Lucas, Weinberg et Clowes

3. x<-0:45 # no vendeurs

4. a=1

5. b1=0.43

6. b2=-0.29

7. P=61000 # Potentiel global

8. W=69 # charge de travail globale

9. y<-a*x*(P/x)^b1*(W/x)^b2 # fonction des ventes (demande)

10. m=2 # marge unitaire

11. C=40 # cout par vendeur

12. profit<-m*y-C*x

13. df<-data.frame(ForceV=x, Ventes=y, Profit=profit)

14. df

15. matplot(x, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits"

16. legend(min(x), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

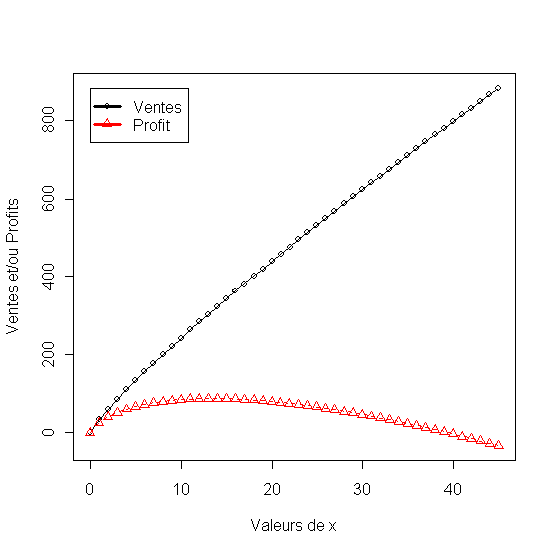
Ce modèle proposé par Lucas, Weinberg et Clowes (1975) exprime les ventes comme un fonction du potentiel du territoire et la charge de travail estimée. Il utilise à la fois une structure linéaire et log-linaire.

La figure motre que le nombre de vendeurs optimum dans l'exemple donné est d'environ 12

Figure 38 - Ventes et Profit en fonction de l'effort de vente (force de vente)

Modèles du mix Marketing

L'interaction du mix

Exemples

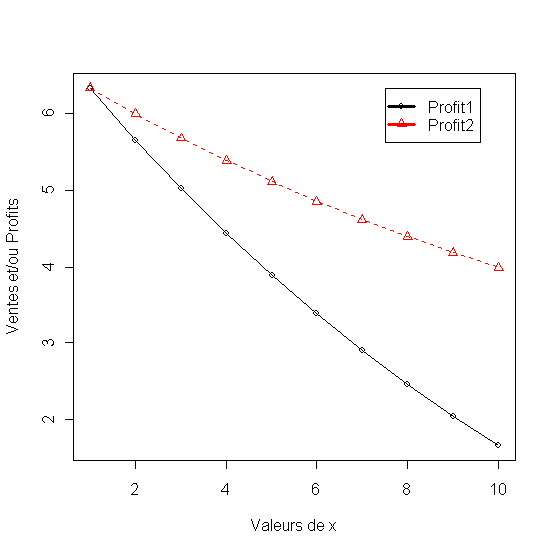
Modèle ou l`élasticité prix est fonction de l`effort publicitaire [ 5.1-3]

En simplifiant l'état des connaissance actuel en la matière on peut dire qu'un publicité déstiné à différencier néttement un produit peut faire baisser l'élasticité aux prix, et qu'un publicité destiné à méttre en valeur le rapport qualité/prix peut accroître cette elasticité.

Listing 35

1. # Modèle ou l`elasticité prix est fonction de l`effort publicitaire

2. x1<-seq(0,5,0.5)

3. x2<-rep(11,11)

4. f1 <- 0.2+2.3*x1^1.5/(3.5^1.5+x1^1.5) # pub 5.2

5. f2 <- 5*x2^(-0.25*(x1-4)) # prix 5.3

6. y<-100*f1*f2 # 5.1

7. profit<-(x2-3)*y-x1

8. df<-data.frame(Pub=x1, Ventes=y, Profit=profit)

9. f2 <- 5*x2^(-0.25*(1.5-4)) # elasticité du prix fixe pour une pub de 1.5

10. y<-100*f1*f2 # 5.1

11. profit<-(x2-3)*y-x1

12. df$Profit2=profit

13. df

14. matplot(x1, df[,3:4], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

15. legend(min(x1), max(df[,3:4]),names(df)[3:4], lwd=3, col=1:2, pch=1:2)

La figure montre un profit optimum quand l'elasticité au prix dépend du niveau de la publicité et un profit croissant quand l'elasticité au prix est fixe et correspond à l'elasticité calculé précédement pour une publicité optimale de 1.5, ce qui explique que les deux courbes du profis ce croisent à ce niveau de publicité.

Figure 39 - Evolution de profit en fonction de la publicité selon que l'élasticité prix s'acccroît avec la publicité ou non.

Modèle de l`usure de la publicité [ 5.4-5]

Listing 36

1. # Modèle de l`usure de la publicité

2. a=10

3. b=10

4. c=-1

5. t<-1:10

6. bt<-b*exp(-0.07*(t-1)) # effet d`usure sur le coef b de la pub

7. xopt<-(1-0.3*b)/(0.6*c) # pub optimum ingorant l`usure

8. x<-rep(xopt,10)

9. y<-a+bt*x+c*x^2

10. profit<-0.3*y-x

11. df<-data.frame(Temps=t, Profit1=profit)

12. xopt_t<-(1-0.3*bt)/(0.6*c) # pub optimum utlisant l`usure

13. x<-xopt_t

14. profit<-0.3*y-x

15. df$Profit2=profit

16. df

17. matplot(t, df[,2:3], pch = 1:2, type = "o", col = 1:2,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

18. legend(mean(t), max(df[,2:3]),names(df)[2:3], lwd=3, col=1:2, pch=1:2)

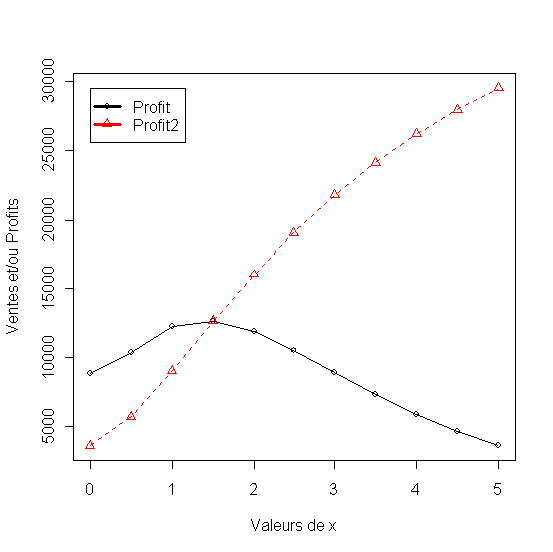
En égalant à zéro la dérivé de la fonction du profit on déduit le budget de publicité optimum à pratiquer. Quand l'usure de la pub qui affecte dans ce cas le coefficient b est ignoré le niveau de publicité optimum reste fixe dans le temps et depend des coefficients initiaux du modèle.

Quand l'usure est prise en compte la publicité optimum n'est pas fixe elle dépend de l'usure dans ce cas du changement dans le temps du coefficient b (qui devient bt). La prise en compte de l'usure a chaque période quand on fixe le budget de publicité à un effet favorable sur les profit tel que l'illustre la figure.

Figure 40 - Profits d'un politique qui prend en compte l'usure la publicité comparée à une politique publicitaire qui prévoit des dépenses constantes.

Budget optimum quand l interaction des variables du mix et positive, negative ou zero [5.6-9]

Listing 37

1. # Variation du budget optimum quand l interaction des variables du mix et positive, negative ou zero

2. a=50

3. b=200

4. c=2

5. d=2

6. x1<-seq(6,7.9,0.1)

7. x2<-rep(7,20)

8. f1<-a+(b-a)*x1^c/(d^c+x1^c)

9. f2<-a+(b-a)*x2^c/(d^c+x2^c)

10. y<-f1+f2 # sans interaction

11. profit<-0.3*y-x1-x2

12. df<-data.frame(Effort=x1, Profit.InteractZero=profit)

13. y<-f1+f2+0.001*f1*f2 # interaction positive

14. profit<-0.3*y-x1-x2

15. df$Profit.InteractPos<-profit

16. y<-f1+f2-0.001*f1*f2 # interaction negative

17. profit<-0.3*y-x1-x2

18. df$Profit.InteractNeg<-profit

19. df

20. matplot(x1, df[,2:4], pch = 1:2, type = "o", col = 1:3,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

21. legend(0.75*max(x1), max(df[,2:4]),names(df)[2:4], lwd=3, col=1:3, pch=1:3)

Figure 41 - Profits quand l'interaction des variables du mix et positive, negative ou zero

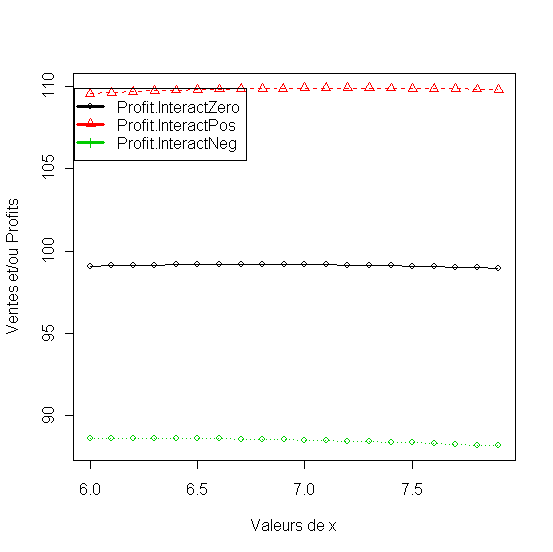
Réaction de la concurrence

Exemples

Modèle de concurrence [5.10-12]

Listing 38

1. # Modèle de Concurrence

2. nx1<-seq(6,10.5,0.5)

3. nx2<-rep(2,10)

4. nattr<-(5*nx1^-2)*(0.3+2*nx2^2/(2^2+nx2^2))

5. cx1<-rep(9,10)

6. cx2<-rep(2,10)

7. cattr<-(5*cx1^-2)*(0.3+2*cx2^2/(2^2+cx2^2))

8. npart1<-nattr/(nattr+3*cattr) # notre part - cas de référence

9. npart2<-nattr/(nattr+6*cattr) # notre part - marché plus large plus de concurrents

10. y<-1600*(cx1+cx2)^-1.5

11. profit1<-npart1*y*(nx1-3)-nx2

12. profit2<-npart2*y*(nx1-3)-nx2

13. df<-data.frame(Effort=nx1, Part1=npart1, Profit1=profit1, Part2=npart2, Profit2=profit2)

14. #Politique de pub agressive de la concurence par rapport à notre prix

15. cx2<-ifelse(nx1>=9,cx2,cx2+(9-nx1))

16. cattr<-(5*cx1^-2)*(0.3+2*cx2^2/(2^2+cx2^2))

17. npart3<-nattr/(nattr+6*cattr) # marché large

18. profit3<-npart3*y*(nx1-3)-nx2

19. df$Part3<-npart3

20. df$Profit3<-profit3

21. df

22. matplot(nx1, df[,c(3,5,7)], pch = 1:3, type = "o", col = 1:3,xlab="Valeurs de x", ylab="Ventes et/ou Profits")

23. legend(min(nx1), max(df[,c(3,5,7)]),names(df)[c(3,5,7)], lwd=3, col=1:3, pch=1:3)

La figure montre l'evolution de nos profits en fonction du buget de publicité pratiqué dans trois situation diférentes: 1) quand le marché est petit avec seulement 3 concurrents, 2) quand le marché est plus grand avec 6 concurrents (dans les premiers deux cas notre publicité est 2 et egale à celle des concurrents, et le prix des concurrents est 9), 3) quand le marché est grand et les concurents pratiquent une politique publictaire agressive par rapport à nos prix (quand nos prix sont en dessous de 9 ils ajoutent à leur buget de pub un somme égale à deux fois notre reduction de prix).

Figure 42 - Analyse du prix optimal sous trois hypothèses sur la nature de la concurrence

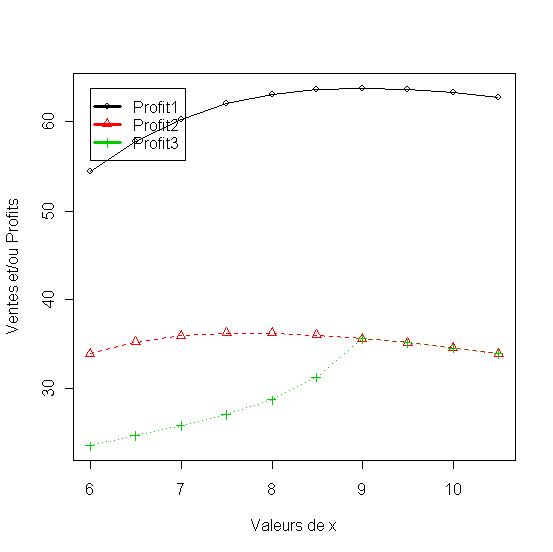
Estimation des modèles

Présentation

Estimer un modèles signifie attribuer des valeurs aux paramètres du modèle. Pour qu'un modèle soit réaliste et capable d'offrir de l'aide à la décision il doit reposer sur des mesures. Ces mesure s'appuyent sur des données récoltées directement ou indirectement.

On peut distinguer de catégories de méthodes d'estimation des modèles, l'estimation objective et subjective. L'estimation subjective se distingue par le faite que le données qu'elle utilisent reposent sur des jugement d'experts.

Estimation objective

Présentation

L'estimation objective utilise des données pour paramétrer des modèles.

[A faire .. parler des sources de données en marketing, (pimaires, secondaires), enquetes, panels de consommateur et distributeur etc.]

Régression linéaire

Présentation

Exprime la corrélation entre la variable expliquée y et une ou plusieurs variables explicatives Xi par une équation ayant le format général:

y = f(xj) + e

ou e est l'erreur d'approximation

L'estimation par régression linéaire est facilement calculable et la plupart des calculettes et des tableurs disposent de fonctions spécialisées. Pour une illustration de l'utilisation du logiciel R on peut se référer à l'utilisation de la régression linéaire dans les modèle de régression des préférences et d'analyse conjointe utilisés dans la partie de ce document qui traite des modèles de choix des caractéristiques des produits.

Le modèle linéaire

Si la corrélation est linéaire alors

y = ao+ a1x1+ a2x2 + ... + akxk;

exprime de manière matricielle cela correspond à:

y =

Organisation des données

si on entasse tous les observations de y dans un vecteur, on obtient:

y = Xa + e

= +

La MCO

Disposant de séries de données pour les valeurs de y, x1, x2 etc. on peut calculer les valeurs des coefficients ao, a1, a2 etc. telle que f(xj) (qu'on va appeler tout simplement f) approxime au mieux la corrélation existante. Autrement dit la moyenne de ses erreurs en valeur absolue doit être minime, ce qui équivaut à la minimisation de la somme de ses carrées. De la formule générale on déduit que l'erreur au moment i noté ei est égale à yi-fi et la somme des moindres carrés est

min e_i²= (y_i-f_i)² =(y_i-(a_o+ a₁x_1i+ a₂x_2i + a_kx_ki))².

ou sous forme matricielle:

Min(y - Xa)' (y - Xa)

Solution algebrique

La minimisation des carrées est obtenue en égalant a zéro les dérivées partielles de ces expressions en fonction de ao, a1, a2...an ce qui a comme résultat le suivant système d'équations:

na_o + a₁Sx₁ + a₂Sx₂ + ......... a_kSx_k = S_y

a_oS x₁ + a₁S x₁x₁ + a₂S x₂x₁ + .... a_kS x_kx₁ = S yx₁

a_oS x₂ + a₁S x₁x₂ + a₂S x₂x₂ + .... a_kS x_kx₂ = S yx₂

.. .. .. ......

a_oS x_k + a₁S x₁x_k + a₂S x₂x_k + .... a_kS x_kx_k = S yx_k

ou S =

Solution matricielle

ou sous forme matricielle:

(X'X)a = X'y

Les solutions du système sont les coefficients du vecteur a: ao, a1, a2, ....an.

a =(X'X)-1 X'y

Ayant les des valeurs possibles des variables explicatives xj on calcule la valeur de la fonction f(xj) qui représente la prévision de la variable expliquée y.

Indicateurs statistiques

Variation non expliquée	(VN = S (Y-Yc)2)
Variation expliquée	(VE = S (Yc-)2 )
Variation totale	(VT = S (Y- )2)
Coefficient de détermination multiple	(R2 = VE/VT)
Coefficient de corrélation multiple	(R)
Variance expliquée (factorielle)	S2F = 1/k*VE
Variance non expliquée (résiduelle)	S2R = 1/(n-k-1)*VN
Erreur standard de la régression	SR
Test en F	F = S2F/S2R
Erreur standard (Ecart type) de b1	Sb1 =
Erreur standard (Ecart type) de b2	Sb2 =

Estimation par régression linéaire des modèles non-linéaires linéarisables

Modèles	Formulation nonlinéaire	Formulation linéarisée
Racine fractionelles	Q = a_o + a₁ X^a2...	ln(Q-a₀)=ln(a₁)+a₂ln(x)
Exponentiel Modifié	Q = a_o(1 -) + a2	ln(a₀+a₂-Q)=ln(a₀)-a₁X
Logistique	Q = + a₃	ln((Q-a₂)/(a₀-Q+a₂))=a₁+a₂x
Gompertz	Q = ao+a3	ln(ln(a₀)-ln(Q-a₂))=ln(-ln(a₁))+ln(a₂)x
Adbudg	Q = a₁ + (a_o - a₁)	ln((a₀-Q)/(Q-a₁))=a₂ln(a₃)-a₂ln(x)
Log-Linéaire	Q = ao	ln(Q)=ln(a₀)+a₁ln(x₁)+a₂ln(x₂)+ ..

Régression non-linéaire

Presentation

Méthode Newton-Gauss

Méthode du Gradient

Le gradient de plus grande pente

Le gradient conjugué

Méthode Levenberg-Marquard

Méthode Simplex

Les polynômes orthogonaux

Estimation pour variables dépendantes binaires

Estimation Logit

Estimation Probit

Solution d'équation multiples

2SLS

Modèles causaux et variables non observées

Presentation

LISREL, PLS

Estimation subjective (decision calculus)

Presentation

Calibrage du modèle à partir d'un seul expert

Méthodes d'agrégation (pooling) des estimations individuelles par le choix de l'analyste

Méthodes d'agrégation (pooling) des estimations individuelles par le choix du groupe

Groupe coopérative (consensuel)

Méthode Delphi

Combiner les données de jugement et empiriques : estimation Bayesienne

Illustration decision calculus: (locale) (distant)

Bibliographie

Gary Lilien (1987) Analyse des Décisions Marketing (avec Lotus 1-2-3), Economica,

G. Lilien, Ph. Kotler et K. S. Moorthy (1992) "Marketing Models", Prentice Hall, Englewood Cliffs, New Jersey.

J. Eliashberg et G.L. Lilien (Eds.) (1993) Handbooks in Operations Research and Management Science, Vol. 5, Marketing, Elsevier Science Publishers BV.

Notes

1 La plupart des modèles sont adaptés de l'ouvrage de Gary Lilien "Analyse des Décisions Marketing (avec Lotus 1-2-3)" traduit en français par Pierre Desmet et publié aux éditions Economica en 1987.

2 Le système S est un langage de très haut niveau et un environnement d'analyse de données et graphiques. C'est le seul système statistique à avoir reçu le prestigieux Software System Award (1998) de la Association for Computing Machinery (ACM) qui lui reconnaît le mérite d'avoir « définitivement changé la manière dans laquelle les gens analysent, visualisent et manipulent les données ».