La courbe du profit cumulé est unimodale elle atteint un maximum au niveau de quatrième décile.
|
|
Les 24390 clients et prospects de la base de données sont organisés en deux échantillons, les premiers deux tiers forment l'échantillon d'estimation sur lequel les modèles seront calibres et le dernier tiers est mis à part comme l'échantillon test pour vérifier la performance prédictive des modèles Listing 1
Tableau 1 - Descriptif de la BD clients et des échantillons d'estimation et validation
‘‘Conventionellement’’ le nombre d'acheteurs suggéré dans la littérature comme minimum pour calibrer un modèle significatif doit dépasser 500 acheteurs, voir même s'approcher de 1.000—(voir par exemple Nash 1993, p. 143). |
|
|
Dans le contexte de cette étude les variables utilisées sont uniquement de variables comportementales, de type RFM (Récence, Fréquence et Montant). Sept variables de type RFM ont été construites à partir de l'historique d'achat : deux sont des mesures de récence (R1 et R2), deux autres mesurent la fréquence (F1 et F2), et trois variables expriment le montant (M1, M2, M3). Elles sont décrites dans le tableau 2. Tableau 2 – Définition des variables de la famille RFM
|
|
|
Les valeurs des variables RFM ainsi définies ont été calculées pour les sept saisons. Elles serviront pour expliquer l'incidence d'achat. Pour permettre la mise en évidence des effets saisonniers, la relation de causalité entre les variables RFM et l'incidence d'achat sera estimée par les différentes méthodes de ciblage retenues en considérant à chaque fois un décalage d'une et de deux saisons entre la variable dépendante et les variables indépendantes. Afin de pouvoir alterner ces décalages tout-en conservant un historique d'achat suffisant nécessaire à la définition d'une partie des variables RFM, les modèles d'incidence d'achat seront uniquement estimés pour les trois dernières saisons. |
|
|
Un premier groupe de modèle s' intéressent à l'incidence de l'achat. Il permettent d' estimer la probabilité d' achat de chaque client et/ou prospect. On parle aussi de modèles de choix binaire, car la variable expliquée (dépendante) est du type oui/non et codé 0/1: 0 pour ‘‘non’’ (ex. non-achat), 1 pour ‘‘oui’’ (achat). La plupart de modèles qu' on utilise ici ont comme résultat l' estimation d'une probabilité de réponse pour chaque client et/ou prospect dans la base de données. Parmi les modèles estimés on trouve les modèles logit et probit, l'analyse discriminante, les réseaux de neurones et les arbres de régression et classification (CART) |
|
|
les modèles logistiques de type probit ou logit ont l'avantage d'être bien adaptés aux problèmes de décision binaire (achat/non-achat) et d'éviter les désavantages du modèle linéaire de probabilité. Ils sont fréquemment utilisés dans le marketing des bases de données ("database marketing"). Ils supposent l'existence d'une variable latente qui mesure la propension de répondre. Elle dépend d'une série de caractéristiques individuelles représentées dans ce contexte par les variables RFM. Par rapport aux RNA, ces modèles ont l'avantage d'être faciles à interpréter et ils sont connus pour être robustes et donner de bons résultats dans les études comparatives. Listing 2
Analyse: La formule qui exprime la relation entre l'incidence de l'achat (if_cde97) et les variables rfm est utilisé pour calibrer le modèle logit dans le cadre de la procédure de régression linéaire généralisée (GLM). Le modèle logit est la variante par default dans la famille des modèles binomiaux. Pour verifier les performances predictives et economiques du modèle calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). |
|
|
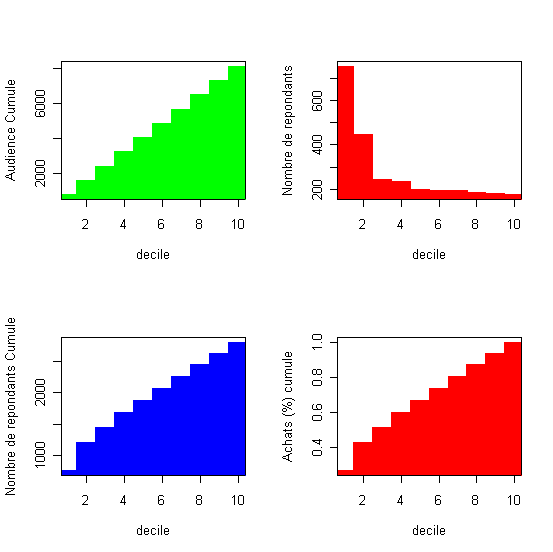
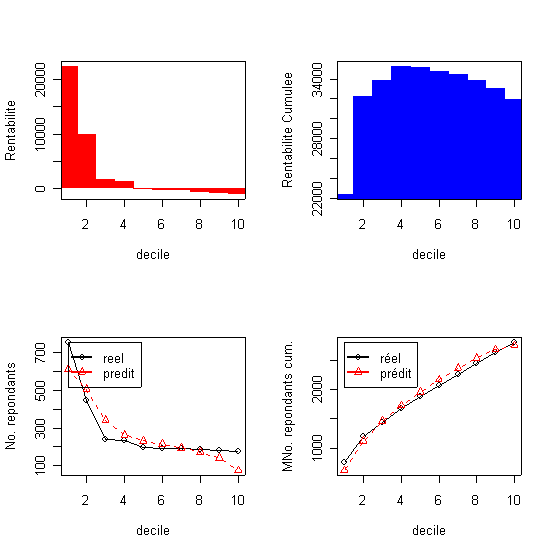
Le tableau présente le résultat des estimation par la régression logistique, appliquée à l'échantillon test, dans l'ordre décroissante de la réponse par décile. Ce tableau est souvent appelé tableau des gains. (dans le Table 2, et dans tous les autres tableaux, Cum. signifie commutatif ..).La probabilité dans la colonne 1 représente la limite inférieure de chaque décile ou autrement dit l'equivalent de la probabilité d'achat du dernier individu dans chaque décile. Le tableau donne aussi le profit évalué au niveau de chaque décile calculé en multipliant le nombre de répondants dans le décile avec le revenu moyen par commande qui lui est égale à la marge de 10% multipliée au prix moyen de 385F (à traduire en euros !!!) et en déduisant les coûts de mailing (ici 10F). decilp cumaud actnresp actcumnresp actcumbuyprc actprofit Analyse: Le taux de réponse d'équilibre (TRE) est égale ici a 10/(0,1*384,91)=25,98% ). Dans ces conditions il convient d'envoyer les mailings aux premiers 4 déciles ou à 3252 clients qui récupèrent 1681 réponses ou 59,86% des achats et un profit total de 23775F. La qualité de la prédiction du modèle logistique est exprimée par le pourcentage des acheteurs qui décline ici fortement avec les décile, de 756 dans le premier deciles à 175 dans le dernier decile(et le nombre prédit de répondants dans chaque décile ce trouve dans les limites de l' intervalle de confiance de 95%...) |
|
|
La courbe du profit cumulé est unimodale elle atteint un maximum au niveau de quatrième décile. |
|
|
> summary(rfm.logit)
|
|
|
La seule différence entre les modèles de réponse logit et probit réside dans la distribution du terme d'erreur qui suit une loi normale pour le modèle probit et une loi logistique pour le modèle probit. Listing 3
Analyse: La formule qui exprime la relation entre l'incidence de l'achat (if_cde97) et les variables rfm est utilisé pour calibrer le modèle probit dans le cadre de la procédure de régression linéaire généralisée (GLM). Le modèle probit est une option dans la famille des modèles binomiaux. Pour verifier les performances predictives et economiques du modèle calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). |
|
|
Prévision sur l'échantillon test decilp cumaud actnresp actcumnresp actcumbuyprc actprofit |
|
|
|
|
|
> summary(rfm.probit)
|
|
|
Conceptuellement, l'analyse discriminante s'éloigne assez fortement des méthodes précédentes car elle tente de trouver une fonction assurant la meilleure discrimination entre répondants et non-répondants. Elle présente l'avantage d'offrir des repères capables d'indiquer si les sujets sont mal classés. En même temps, c'est une technique très sensible aux violations des présomptions de normalité pour des taux de réponses inférieurs à 10% (Shepard, 1995), très fréquents en marketing direct. Listing 4
Analyse: La formule qui exprime la relation entre l'incidence de l'achat (if_cde97) et les variables rfm est utilisé pour calibrer la fonction discriminante dans le cadre de la procédure d'analyse discriminante linéaire (lda). Pour verifier les performances predictives et economiques du modèle calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). Le score de chaque individu sur l'axe discriminant a été transformés en probabilités |
|
|
decilp cumaud actnresp actcumnresp actcumbuyprc actprofit |
|
|
|
|
|
> rfm.lda |
|
|
Le RNA utilisé ici est de type feedforward entraîné avec l'algorithme de rétro-propagation classique (Rumalhart et McCleelland, 1986). « On peut considérer les réseaux de neurones feedforward comme des modèles de régression non-linéaires dont la complexité peut être changée » (Bentz et Merunka, 2000, p.183). Le modèle final de RNA comportait sept variables RFM dans la couche d'entrée, un neurone dans la couche de sortie et quatre neurones dans la couche cachée. Une couche cachée est suffisante pour capter les non-linéarités qui peuvent se trouver dans des problèmes de ciblage de ce type. Pour rendre cette étude comparable avec d'autres études utilisant le même type de variables RFM, le nombre de neurones dans la couche cachée a été fixé à quatre. Cela semble suffire et permet d'éviter des risques de sur-calibrage (overfitting) qui ont un effet négatif sur le pouvoir de généralisation et implicitement sur le pouvoir prédictif du RNA. Plusieurs essais avec un plus grand nombre de neurones ont été réalisés mais les résultats sur la qualité de l'ajustement aux données ne se sont pas améliorés de manière significative. Le nombre de poids à estimer dans une telle architecture est égale à : [ (1 + Nombre d'entrées)*Nombre de neurones cachés] + [(1 + Nombre de neurones cachés)*Nombre de sorties], c'est-à-dire (1+7)*4 + (1+4)*1=37. Ces poids sont initialisés aléatoirement dans l'intervalle (-0.1,0.1). Le processus d'entraînement s'arrête après un nombre d'époques fixées ici à 500, ou avant si le niveau de précision est atteint. (!! En parallèle un autre modèle RNA, qualifié de multiple est obtenu en entraînant successivement et sur les mêmes données dix modèles RNA pour retenir le meilleur. Le nombre d'époques est fixé dans ce cas à 200. Les deux modèles sont complémentaires car le deuxième en reprenant l'entraînement plusieurs fois avec des poids qui s'initialisent avec de valeurs différentes permet d'éviter certains optimums locaux) . La standardisation des variables en entrée améliore la stabilité du processus d'entraînement, car le réseau n'est pas obligé d'opérer avec des poids qui ont des ordres de grandeur différents. Listing 5
Analyse: La formule qui exprime la relation entre l'incidence de l'achat (if_cde97) et les variables rfm est utilisé pour entrainer le réseau de neurones de type backpropagation multylayer perceptrion et pour définir le nombre de neurones dans la couche d'entrée (7+1) et dans la couche de sortie (1). La taille de la couche caché (4 neurones) et le nombre d'iteration maximum sont spécifiés avec la procédure . Pour verifier les performances predictives et economiques du réseau entrainé sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). |
|
|
decilp cumaud actnresp actcumnresp actcumbuyprc actprofit actprofitcum |
|
|
|
|
|
> summary(rfm.nn) |
|
|
Une dernière catégorie de méthodes utilisée dans cette étude comparative est représentée par la méthode des arbres de classification et de régression CART. Développée par Breiman et al (1984), elle remplace souvent les autres méthodes de classification explicative telles que CHAID (Kass, 1980) ou AID (Sonquist, 1970) car elle n'est pas limitée à des variables indépendantes catégorielles (nominales) mais accepte aussi des variables continues3. La fonction rpart, c'est-à-dire l'implémentation de la méthode CART en R a été utilisée pour obtenir un arbre de classification et de régression à partir des données. Il s'agit d'un arbre de classification car la variable dépendante est catégorielle (achat/non-achat) et que l'on traite les données individuelles. Le modèle est obtenu en utilisant toute les variables RFM ; le critère de séparation est la réduction de l'entropie, un minimum de 20 observations dans un nœud terminal (feuille), un paramètre de complexité de 0,001 et une profondeur maximum de l'arbre de 30. L'arbre à 26 noeuds de la saison 7 utilise dans l'ordre les variables R1, F1, et R2 pour séparer les segments ; la variable F2 et les variables R1, R2 et R3 qui représentent la récence apparaissent à des niveaux inférieurs dans la structure de l'arbre. La variable F1 est le plus souvent en première position, suivi par R1 dans la majorité des saisons analysées. Cela est en accord avec le poids de ces variables dans les modèles logit, probit et d'analyse discriminante ajustés. Dans CART tous les clients qui appartiennent au même segment sont traités de la même manière contrairement aux autres méthodes, qui attribuent un score de vraisemblance de réponse différent à chaque client, ce qui leur donne une meilleure granularité par rapport à CART. Listing 6
Analyse: La formule qui exprime la relation entre l'incidence de l'achat (if_cde97) et les variables rfm est utilisé pour calibrer l'arbre dans le cadre de la procédure des arbres de regression et de partitionement recoursif (rpart). Une representation graphique de la segmentation qui résulte donnée dans la figure xx. Pour verifier les performances predictives et economiques de l'arbre calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). |
|
|
decilp cumaud actnresp actcumnresp actcumbuyprc actprofit actprofitcum |
|
|
|
|
|
> summary(rfm.rpart)
|
|
|
La régression ordinale correspond à un modèle de choix discret ou les valeures qui représentent les multiples choix expriment un ordre ou une préférence. Si on choisit le montant des commandes comme variable à expliquer, on peut transformer cette variable continue en variable discrète en ordonnant ses valeures dans des intervalles de choix mutuellement exclusifs et en attribuant à chaque intervalle une catégorie ordinale. Le modèle de régression ordinale peut être utilisé ensuite comme un proxy pour la régression linéaire (Levin et Zahavi, 1998, p.10). Si on se résume à seulement deux catégories ordinales: 0 pour les non-acheteurs et 1 pour les acheteurs, alors les prédicteurs qui résultent de la régression ordinales devraient être identiques à ceux de la régression logistique. En pratique on préférera d'utiliser plusieurs catégories de choix (0, 1, 2 3) affin d'obtenir des résultats plus nuancés. Dans cet exemple les catégories de choix sont définies selon les critères évoqués dans le tableau 3.
Listing 7
Analyse: A part d'estimer une probabilité de réponse générale par client la régression ordinale calcule aussi une probabilité de réponse pour chaque modalité de choix. Les coefficients des variables explicatives sont les mêmes pour toutes les modalités de choix. Le seul élément qui diffère est le terme constant dans l'équation de régression. La formule qui exprime la relation entre les catégories ordinales (if_cde97) et les variables rfm est utilisé pour calibrer le modèle de regression ordinale à l'aide de la procédure proportional odds regression (polr). Pour verifier les performances predictives et economiques modèle ordinal calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). |
|
|
decilp cumaud actnresp actnresp1 actnresp2 actnresp3 actcumnresp Analyse: En tenant compte du taux de réponse d'équilibre calculé auparavant (10/(0,1*387)=25,8%) on devrait sélectionner comme cible les cinq premiers déciles qui regroupent 1921 répondants repartis entre les trois catégories de choix de la manière suivante: 724, 681, 516 . En utilisant les montant moyens qui correspondent à chaque catégorie de choix et les couts de mailing aux 5 premiers déciles (5*813) le profit espéré devient: 10%*(724*168,10F+681*335,13F+516*759,43F) - 5*813*10F = 33530,02 F C'est un profit legèrement inférieur aux profits calculés pour les modèles d'incidence de l'achat. Il est dificile d'offrir d'emblé une comparaison des performances en terme de profit entre le modèle ordinal et les modèle d'incidence de l'achat, même si dans l'ensemble les probabilités de réponse sont les mêmes, car pour la regression ordinale le profit total espéré dépend de la distribution de revenu pour chaque alternative de choix (Levin et Zahavi, 1998, p. 11). C'est un element d'information suplémentaire qui n'est pas prix en compte par les modèles d'incidence de l'achat. (. en terme de qualité de l'ajustement et de performances prédicitve les différences ne sont pas significatives entre les modèles évoqués) |
|
|
|
|
|
> summary(rfm.ordreg) |
|
|
C'est la méthode la plus facile à mettre en place pour estimer de modèle de choix continu car largement disponible sur une gamme large de machines (des calculettes aux ordinateurs) et de logiciels accessibles, comme par exemple les tableurs. Malgré la disponibilité elle n'est pas bien adaptée pour des modèles de choix continu . Les estimations qu'elle fournit ne sont pas bornés par de seuils inférieurs et supérieurs et produisent des profit négatifs pour les individus que se trouvent en bas de la liste. En plus la somme des réponses (profit) réeles est égaleà la somme de réponses prévues. Cela entraine une surestimation des performances de meilleurs clients qui va compenser la sousestimation des perfomances des "mauvais" clients qui pour certains se voient attribuer des valeurs négatives. Listing 8
Analyse: La formule qui exprime la relation entre montant d'achat (ca97) et les variables rfm est utilisé pour calibrer un modèle linéaire dans le cadre de la procédure de régression linéaire (LM). Pour verifier les performances predictives et economiques du modèle calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). |
|
|
decilp cumaud actnresp actcumnresp actcumbuyprc actprofit actprofitcum Analyse: En tenant compte du taux de réponse d'équilibre calculé auparavant (10/(0,1*387)=25,8%) on devrait sélectionner comme cible les cinq premiers déciles qui regroupent 1921 répondants repartis entre les trois catégories de choix de la manière suivante: 724, 681, 516 . En utilisant les montant moyens qui correspondent à chaque catégorie de choix et les couts de mailing aux 5 premiers déciles (5*813) le profit espéré devient: 10%*(montants cumulés)- 5*813*10F = 35961.4F C'est un profit sensiblement supérieur aux profits calculés pour les modèles d'incidence de l'achat. Il est dificile d'offrir d'emblé une comparaison des performances en terme de profit entre les modèles de choix continu comme la regression linéaire et les modèles d'incidence de l'achat, même si dans l'ensemble les probabilités de réponse sont les mêmes. Si dans les modèles de choix continus le profit total espéré dépend de la distribution des montants individuels par rapport aux quantiles (déciles) dans les modèles de l'incidence de l'achat le montant individuel d'achat est constant et fixé à la moyenne enregistrée par les commandes. La courbe des profit cumulés n'est pas unimodale, les déciles 3 et 5 avec des profits négatifs intrérompent la croissance profits cumulés. Le profit optimum est atteint au décile 4 (36277.1F) et un deuxième pique proche du optimum est atteint au decile 6 (36028.9F). Comparé à la fonction de profit du modèle logit les résultats de la regression linéaire permetent moins de mailings pour plus de profit. Levin et Zahavi (19989 ont trouvé l'inverse. Ces différences et les oscillations qui se manifestent dans la courbe des profits cumulés peuvent être attribués à la faible performance prédictive du modèle de regression linéaire et au nonlinéarités qui caractérisent les données. La qualité de l'ajustement d'un modèle continu peut être vérifié en comparant la colonne des montants moyens par decile cumulés réels et predits (actcumnresp, |
|
|
|
|
|
> summary(rfm.linreg) |
|
|
La regression linéaire considère que la variable dépendente est observé dans tout les cas, mais en réalité en marketing direct elle est observé uniquement pour les répondants. On observe le montant de la commande uniquèement pour les gens qui ont commande suit à une campagne. Il n'y a pas d'observations sur le montant d'achat pour ceux qui n'ont pas commandé. On dit que la variable de réponse est "censuré" à gauche. La variable prend donc une valeur positive pour les répondants et la valeur zéro pour les nonrépondants et ne satisfait donc pas la condition d'être normalement distribué, comme l'exige la regression linéaire. Le modèl Tobit est un modèle de regression qui prend en compte de manière explicite le faite que la valeur de la réponse est observée uniquement pour les répondants, qui sont une petite minorité dans la population dans les application de database marketing. Les résultats d'un modèle tobit sont exprimé sous forme de valeur de choix continue, ici en termes de montants des comandes par client. Listing 9
Analyse: La formule qui exprime la relation entre le montant d'achat (vu comme une valeur censuré à gauche dans le sens des modèles de survie) et les variables rfm est utilisé pour calibrer un modèle de type tobit dans le cadre de la procédure de régression de survie(survreg). La distribution des réponses (montant), y compris des réponses censurées est considéré normale (gaussiene). Pour verifier les performances predictives et economiques du modèle calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). Comme les valeurs censurées sont supposées négatives et majoritaires, le valeures prédites sont en grand partie négatives (ici on les a décalé en r'ajoutant un facteur d'echelle !! ... ) |
|
|
decilp cumaud actnresp actcumnresp actgains actcumgains actcumbuyprc Analyse: |
|
|
|
|
|
> summary(rfm.tobit) |
|
|
Comme dans la régression linéaire le modèle Tobit suppose que la variable de réponse peut prendre toute valeur, même des valeurs négatives mais comme ces dernieres ne sont pas disponibles car il n'y a pas des observations pour les non-répondants elles sont censurées et substitués par la valeur zéro. Cela n'est pas très réaliste car en marketing direct les réponses égales à zéro survienent parceque certains clients choisissent de décliner l'offre et non pas parceque la réponse était négative et par conséquence censurée à zéro. Pour subvenir à ce problème que présente le modèle Tobit une solution alternative est d'estimer une répons continue en deux étapes en utilisant le modèle à deux niveaux de Heckman (1979). Dans un première étape on applique un modèle de choix binaire (ex. logistique) à toutes à l'échantillon d'estimation. Ensuite un modèle linéaire est estimé uniquement au niveau de répondants pour estimer la réponse (conditionelle) espéré par client à condition que celui-ci soit un répondant Ensuite un modèle la réponse (inconditionnelle) espérée par client est obtenue en multipliant la réponse conditionnelle par la probabilité d'achat. Le modèle à deux étapes souffre du biaïs de séléctions car il est basé uniquement sur les répondant et ne constitue donc pas un échantillon aléatoire de la population. Listing 10
Analyse: La probabilité d'achat donnée par le modèle logit estimé auparavant, est calculée pour chaque individu présent dans l'échantillon d'estimation. Elle servira comme variable explicative supplémentaire dans la regression effectuée en deuxieme etape. La formule qui exprime la relation entre le montant d'achat (ca97), les variables rfm auxquelles et la probabilité d'achat (estimé dans la premiere étape) est utilisé pour calibrer un modèle linéaire dans le cadre de la procédure de régression linéaire(LM). Pour verifier les performances predictives et economiques du modèle calibré sur deux tiers des clients on effectue les calculs prédictifs sur le tiers complémentair et on calcule le tableau des gains (gainchart). Loading required package: tcltk |
|
|
decilp cumaud actnresp actcumnresp actgains actcumgains actcumbuyprc |
|
|
|
|
|
> summary(rfm.2stage) |