Particularités des modèles logit
Par contre l'interprétation du coefficient b quant à son influence sur p est plus délicate : elle varie selon la variable X (variable centrée) comme cela est illustré dans le diagramme suivant.
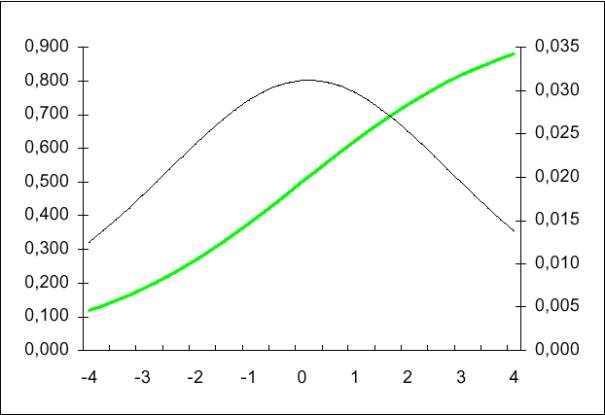
La courbe en forme de cloche indique la variation de la probabilité pour 1/4 d'unité de X. On se rend compte que l'impact maximal est obtenu autour de X=0, et que plus la valeur absolue de X est grande moins l'impact est important. Il en résulte qu'il est difficile d'interpréter la valeur b directement. C'est pourquoi, on peut être tenté d'utiliser un autre indicateur dont l'effet soit constant.
Si l'on réécrit le modèle sous la forme suivante :
p/(1-p)= eZ
= ![]()
On s'aperçoit que la quantité exp(b) représente le facteur par lequel le rapport p/(1-p) augmente lorsque X varie d'une unité. Cette quantité est indépendante de X. Ainsi, avec cette expression on obtient une valeur de paramètre qui est plus interprétable que le b dans la forme linéarisée (il est difficile de se représenter un logit) et qui n'a pas l'inconvénient souligné précédemment dans la forme non-linéaire.
Dans l'exemple précédent le coefficient b était égal à 0,5. Exp(0,5)=1,64. Ceci signifie que pour une augmentation de une unité de X, le rapport p/(1-p) est augmenté de 1,64 fois. Si b=0, exp(b)=1, le rapport reste inchangé, ce qui signifie simplement que les probabilités ne dépendent pas de X. Si b est égal à 0, exp(b) sera inférieur à 1, ce qui signifie simplement que l'effet est négatif.









