La méthode du maximum de vraisemblance
Plutôt que de raisonner en deux étapes, on emploie, une technique d'estimation appelée maximum de vraisemblance. Dans le cadre du modèle logit cette fonction s'écrit :
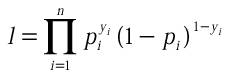
La signification de cette quantité est claire. Si un individu a pour valeur y=1, que la probabilité calculée est de 0.8, la vraisemblance pour cet individu est de 0,81 x 0,2 0 =0,8. Dans le cas contraire (y=0 et même probabilité) on a li=0,2. On se rend compte ainsi que si les estimations des probabilités sont en accord avec l'observation, la vraisemblance est maximisée. Puisque p dépend du vecteur de paramètre β et du vecteur de variable X, on va chercher à maximiser la vraisemblance en les manipulant. Naturellement on ne pourra pas toucher au vecteur X, car ce sont les données. Par contre on cherchera quelles sont les valeurs de β qui maximisent cette quantité l.
D'un point de vue pratique, il est plus commode d'utiliser la log-vraisemblance, notée L, celle-ci transformant les produits en somme. Maximiser cette quantité, revient à maximiser la vraisemblance.
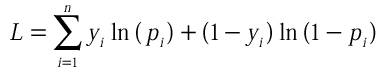
A partir de ce moment le problème devient simple, puisque pour trouver le maximum de cette fonction, il suffit d'égaler sa dérivée à 0. En pratique, on utilise des méthodes numériques telles que l'algorithme de Newton-Raphson, pour trouver les valeurs recherchées.









