Dans la mesure où une question peut
relever fondamentalement de trois niveaux de mesure différents,
on comptera neuf types de croisements possibles entre les questions
![]() et
et
![]() Les plus fréquentes sont présentés ci-dessous.
Les plus fréquentes sont présentés ci-dessous.
2 -
![]() quantitatif x
quantitatif x
![]() quantitatif: étude des relations entre deux séries
de n chiffres s'il y a n questionnaires. Ces deux séries de
chiffres n'apparaissent généralement pas explicitement.
Leurs relations sont matérialisées par différents
indicateurs.
quantitatif: étude des relations entre deux séries
de n chiffres s'il y a n questionnaires. Ces deux séries de
chiffres n'apparaissent généralement pas explicitement.
Leurs relations sont matérialisées par différents
indicateurs.
Exemple:
Dans le questionnaire CAMIP, étude des relations entre le proportion des achats par catalogue (question 1 ) et le revenu de la personne (question 11). L'appartenance à une catégorie de revenu plus élevé entraîne-t-elle une plus grande proportion des achats par catalogue ?
2 -
![]() nominal x
nominal x
![]() nominal : croisement le plus fréquent qui se traduit par
la création d'un tableau de contingence où, en
ligne, figurant les modalités de la variable à
expliquer et en colonne, celles de la variable explicative. Lorsque
le tableau de contingence est traduit en pourcentages de colonne,
pour chaque modalité de la variable explicative apparaîtra
une distribution de fréquences des modalités de la
variable à expliquer.
nominal : croisement le plus fréquent qui se traduit par
la création d'un tableau de contingence où, en
ligne, figurant les modalités de la variable à
expliquer et en colonne, celles de la variable explicative. Lorsque
le tableau de contingence est traduit en pourcentages de colonne,
pour chaque modalité de la variable explicative apparaîtra
une distribution de fréquences des modalités de la
variable à expliquer.
Exemple:
Croisement entre la question 22 sur la préférence pour un type de magasin ou une modalité d'achat et la question 26: le fait de préférer d'acheter par catalogue ou par une autre modalité, dépende-t-elle de la situation civile du répondant?
3 -
![]() ordinal x
ordinal x
![]() ordinal : mise en correspondance de deux classements au niveau de
chaque individu interrogé ou sur l'ensemble de l'échantillon
si une procédure d'agrégation des rangs a été
utilisé.
ordinal : mise en correspondance de deux classements au niveau de
chaque individu interrogé ou sur l'ensemble de l'échantillon
si une procédure d'agrégation des rangs a été
utilisé.
Exemple:
Croisement entre l'ordre de préférence pour les différentes catégories d'équipement de bureau (micro-ordinateurs, imprimantes, scanners..) exprimé par chaque répondant et un classement a priori correspondant à l'importance accordé à chaque catégorie d'équipement dans le catalogue (exprimé par exemple en nombre de pages).
4 -
![]() quantitatif x
quantitatif x
![]() nominal : correspond à un tri-à-plat de la variable
quantitative pour chacune des modalités de la variable
nominale qui joue le rôle de variable explicative.
nominal : correspond à un tri-à-plat de la variable
quantitative pour chacune des modalités de la variable
nominale qui joue le rôle de variable explicative.
Exemple:
Croisement entre une question ouverte concernant le nombre d'objets achetés par catalogue et la question 26. La situation civile influence-t-elle le nombre d'objets achetés par catalogue?
5 -
![]() ordinal x
ordinal x
![]() nominal : repérage des rangs donnés à la
question Qi pour différentes classes d'une variable Qj
nominale explicative.
nominal : repérage des rangs donnés à la
question Qi pour différentes classes d'une variable Qj
nominale explicative.
Exemple:
Croisement entre un classement de préférence et la question 26. Le fait de relever d'un statut familial donné entraîne-t-il des préférences pour une catégorie de produit bureautiques ?
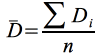 et la variance des différences est alors
et la variance des différences est alors
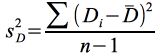
 (21)
(21)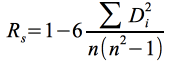 (25)
(25) (26)
(26)