MULTIVAR
un système d'analyse multivariée des données
intégré au tableur
Auteur: Mihai Calciu - Université de Lille
I
MULTIVAR est un système d'aide à
la décision intégré à Excel qui permet l'utilisation
sur tableur des techniques d'analyse multivariée des donnée
les plus utilisés en marketing
Les options proposées sont:
- Vecteurs et Valeurs Propres
- Positionnement
- Analyse Factorielle des Correspondances
- Typologie
- Scoring
- Geo Typologie
Sont rajoutées à Excel douze fonctions matricielles qui permettent
des analyses très flexibles.
L'interface avec l'utilisateur du système MULTIVAR s'inspire de
celle de l'outil d'analyse de données intégré à
la version anglaise de Excel 4 (Analysis Tool) et qui est disponible actuellement
aussi dans la version française de Excel 5.
Organisation des données à traiter
Les données qu'on veut traiter par une méthode d'analyse
multivariée doivent être organisés sur les lignes et
colonnes du tableur pour former le tableau d'entrée (ou la zone
d'entrée). On peut rajouter des étiquettes dans la ligne
et/ou colonne de la première cellule du tableau d'entrée
pour identifier les variables et les observations.
Lors de l'utilisation d'une méthode d'analyse multivariée
le système crée un tableau (zone) de sortie des résultats.
Le contenu du tableau des résultats dépend de la méthode
utilisé. Si on a utilisé des étiquettes dans la zone
d'entrée le système les utilisera pour étiqueter les
données de sortie. Si on n'a pas spécifié des étiquettes
dans la zone d'entrée le système va fabriquer ces propres
étiquettes pour la zone de résultats.
Le traitement des données
Pour utiliser une méthode d'analyse multivariée après
avoir choisi la commande Analyse Multivariée du Menu Option:
1 Sélectez dans la boite de dialogue "Analyse Multivariée"
la méthode que vous voulez utiliser
2 Appuyez sur le bouton OK
3 Indiquez la zone d'entrée, la zone de résultats et
toute autre option proposée par la nouvelle boite de dialogue spécifique
à la méthode choisie.
Les zones de la feuille de calcul peuvent être indiquées dans
les rubriques des boîtes de dialogue comme dans la majorité
des commandes Excel en tapant la référence ou en selectant
le contenu de la rubrique et après en sélectant la zone de
cellules de la feuille. On peut aussi inscrire des références
à d'autres feuilles dans zone d'entrée et de sortie.
4 Appuyez sur OK
Les résultats apparaîtront dans la zone que vous avez désigné
comme zone de résultats.
Présentation des analyses disponibles et de leur mode d'utilisation
Multivar apparaît comme une option dans les Menus de Microsoft Excel
et offre les analyses affichés dans la boite de dialogue présentée
ci-dessous.
Calcule les Valeurs et Vecteurs propres d'une matrice de Variances Covariances
ou d'une matrice de Corrélations. Ce calcule à un rôle
central dans un grand nombre d'analyses multivariées des données
telle que l'analyse factorielle en composantes principales, l'analyse factorielle
des correspondances, l'analyse discriminante.
Il permet, à partir des corrélations (ou covariances) entre
les variables, d'identifier des facteurs qui ne sont pas corrélés
entre eux et qui représentent des combinaisons linéaires
de ces variables.
[IMAGE]
La zone d'entrée doit contenir une matrice symétrique
des corrélations ou des covariances (celle-ci peut être calculée
à partir des données originelles utilisant les fonctions
MatCorrel ou MatCovar selon le cas, ces fonctions doivent être rajoutées
à Excel (pour détails voir la rubrique Installation du paquet
MULTIVAR)).
L'option groupé par indique si les données d'entrée
sont groupées en ligne ou en colonne.
Si l'option Etiquettes en première Ligne ou Colonne est cochée
le programme va prendre les étiquettes qu'il utilisera dans les
tableaux de sortie et dans les graphiques de la première ligne (si
les données sont groupées en colonne) ou de la première
colonne (si les données sont groupées en ligne).
La zone de résultats affiche les résultats dans une
matrice qui contient une ligne et une colonne supplémentaire par
rapport à la zone d'entrée. Dans cette matrice chaque colonne
représente un facteur (axe factoriel) sauf la dernière colonne
qui affiche les variances des variables.
1 dans la partie supérieure de la matrice rangés en
colonnes ce trouvent les vecteurs propres qui expriment les coefficients
de pondération des variables dans la combinaison linéaire
qui forme chaque facteur. Ces coefficients sont utils pour interpréter
les axes factoriels en fonction des variables qui les composent, et pour
calculer les projections des observations sur les axes factoriels.
2 sur la dernière ligne ce trouvent les valeurs propres (eigenvalues)
(de la matrice d'entrée) qui expriment la partie de la variation
(information) observé dans les données expliqué par
chaque facteur. Souvent une nombre réduit de facteurs (2 ou 3) arrivent
à exprimer la plus grande partie de l'information (variation) (60
à 90%) ce qui permet de les utiliser pour résumer l'information
contenue dans un nombre plus important de variables. Ainsi on facilite
la compréhension du phénomène étudié
et on rend possible sa visualisation par l'intermédiaire de cartes.
Permet d'appliquer l'analyse en composantes principales à un tableau
de données numériques afin de réduire le nombre de
variables (colonnes) qui caractérisent les observations (c-a-d.
réduire la complexité de l'information) à un nombre
limité d'axes orthogonales (deux ou trois) permettant de représenter
les observations (mais aussi les variables) dans un espace à deux
dimension et d'obtenir ainsi une carte de positionnement.
Le calcul des valeurs et vecteurs propres est utilisé pour déterminer
la position des observations dans l'espace défini par les axes factoriels
retenus.
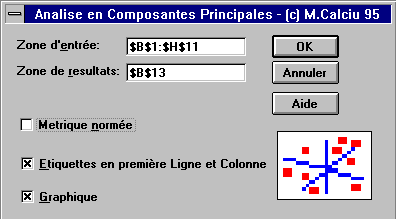
La zone d'entrée doit contenir un tableau ayant sur les lignes
les individus (observations) et en colonnes les valeurs des variables qui
caractérisent chaque individu.
Si l'option Etiquettes en première Ligne et Colonne est cochée
la première ligne et la
première colonne du tableau d'entrée sont utilisées
comme étiquettes pour les individus et les variables.
L'option Métrique indique si la métrique choisie est
canonique ou normée. Si les valeurs des variables ont des ordres
de grandeur différents il est préférable de choisir
la métrique normée.
L'option Graphiques cochée détermine l'affichage de
trois graphiques. Le premier illustre la contribution décroissante
des axes factoriels à l'information totale et indique le nombre
d'axes à retenir. Le deuxième graphique montre les coordonnées
des variables dans le plan factoriel et le troisième les coordonnées
des individus dans le même plan.
La zone de résultats commence dans la cellule indiquée
dans la boite de dialogue et contient trois tableaux rangés en colonnes.
Chaque colonne représente un axe factoriel. Ces axes forment un
système de coordonnés orthogonales sur les quelles on peut
visualiser les variables et les observations.
Le premier tableau est intitulé Valeurs et Vecteurs propres.
1 dans la partie supérieure de la matrice rangés en
colonnes ce trouvent les vecteurs propres qui expriment les coefficients
de pondération des variables dans la combinaison linéaire
qui forme chaque facteur. Ces coefficients sont utils pour interpréter
les axes factoriels en fonction des variables qui les composent, et pour
calculer les projections des observations sur les axes factoriels. La dernière
colonnes affiche les variances des variables.
2 sur les dernières deux lignes ce trouvent les valeurs propres
(eigenvalues) et le pourcentage de variation (information) expliqué
par chaque facteur. Souvent une nombre réduit de facteurs (2 ou
3) arrivent à exprimer la plus grande partie de l'information (variation)
(60 à 90%) ce qui permet de les utiliser pour résumer l'information
contenue dans un nombre plus important de variables. Ainsi on facilite
la compréhension du phénomène étudié
et on rend possible sa visualisation par l'intermédiaire de cartes.
Le deuxième tableau donne les coordonnées des variables
sur les axes factoriels et sert à interpréter les axes en
fonction des variables.
Le troisième tableau donne les coordonnées des individus
sur les axes factoriels. Le graphique obtenu à partir de ce tableau
est la carte de positionnement.
Est une technique de positionnement adapté au donnés catégorielles.
Initialement conçue pour l'étude des tableaux de contingence
(tris croisés) elle est appliqué aussi à des tableau
disjonctifs complets, des tableaux de données ordinales et même
à tout tableau de données positives. La méthode est
construite pour décrire les lignes et colonnes d'un tableau de contingences
qui correspondent aux modalités de deux caractères qualitatifs
(par exemple la distribution de la préférence pour des marques
en fonction de la catégorie socioprofessionnelle des clients).
[IMAGE]
La zone d'entrée doit contenir un tableau ayant sur les lignes
les modalités d'une caractéristique A et en colonnes les
modalités d'une caractéristique B.
Si l'option Etiquettes en première Ligne et Colonne est cochée
la première ligne et la première colonne du tableau d'entrée
sont utilisées comme étiquettes pour les modalités
des caractéristiques en ligne et en colonne.
L'option Graphiques cochée détermine l'affichage de
deux graphiques le premier représentant les coordonnées des
modalités en colonne dans le plan factoriel et le deuxième
les coordonnées des modalités en ligne dans le même
plan.
La zone de résultats commence dans la cellule indiquée
dans la boite de dialogue et contient trois tableau rangés en colonnes.
Chaque colonne représente un axe factoriel. Ces axes forment un
système de coordonnés orthogonales sur les quelles on peut
visualiser les modalités des caractéristiques en ligne et
en colonne.
Le premier tableau affiche les valeurs et vecteurs propres.
1 dans la partie supérieure de la matrice rangés en
colonnes ce trouvent les vecteurs propres qui expriment les coefficients
de pondération des modalités en colonne dans la combinaison
linéaire qui forme chaque facteur. Ces coefficients sont utils pour
interpréter les axes factoriels en fonction des modalités
en colonne qui les composent, et pour calculer les projections des observations
sur les axes factoriels.
2 sur la dernière ligne ce trouvent les valeurs propres (eigenvalues)
(de la matrice d'entrée) qui expriment la partie de la variation
(information) observé dans les données expliqué par
chaque facteur. Souvent une nombre réduit de facteurs (2 ou 3) arrivent
à exprimer la plus grande partie de l'information (variation) (60
à 90%) ce qui permet de les utiliser pour résumer l'information
contenue dans un nombre plus important de modalités en colonne.
Ainsi on facilite la compréhension du phénomène étudié
et on rend possible sa visualisation par l'intermédiaire de cartes.
Le deuxième tableau donne les coordonnées des modalités
en colonne sur les axes
factoriels et sert à interpréter les axes en fonction des
modalités en colonne.
Le troisième tableau donne les coordonnées des modalités
en ligne sur les axes factoriels.
L'analyse typologique (Cluster Analysis) est une méthode d'identification
des groupes d'individus (répondants) aux profils de réponses
similaires.
Cette commande effectue une classification hiérarchique ascendante
des observations du tableau d'entrée selon leur ressemblance (similarité)
en fonction des variables qui les caractérisent. La similarité
est mesurée en distances euclidiennes entre les observations dans
l'espace des variables (colonnes).
Les observation sont comparées, les plus similaires sont regroupées,
pour former des noeuds ou groupes ou clusters). Les noeuds obtenus et les
observation pas encore groupées, sont comparés et regroupés
de manière itérative, jusqu'au niveau ou toute est groupé
dans un seul noeud. Ce processus de regroupement est donné par le
tableau des résultats. On obtient ainsi une hiérarchie qui
est bien illustré par un graphique nommé dendogramme.
Quatre méthodes d'appréciation des distances entre groupes
peuvent être choisies dans le processus de regroupement:
l La méthode du plus proche voisin (Lien simple).
La distance entre deux groupes I et II est assimilée à la
distance entre les deux éléments les plus proches, l'un appartenant
au groupe I et l'autre au groupe II.
L'utilisation de cette méthode entraîne le risque de faire
apparaître des groupes très hétérogènes,
puisqu'on ne se préoccupe pas des éléments les plus
extrêmes des groupes.
2 La méthode du voisin le plus éloigne (Lien complet)
La distance entre deux groupes I et II est assimilée à la
distance entre les deux éléments les plus éloignés,
l'un appartenant au groupe I et l'autre au groupe II.
3 La procédure du chaînage moyen (Lien moyen)
La distance est calculé à partir du barycentre (ou centre
de gravité) des groupes. Cette méthode paraît plus
logique, mais elle demande beaucoup plus de calculs que les deux précédentes
: chaque regroupement d'individus demande un nouveau calcul de distance,
alors que les autres méthodes utilisent seulement les distances
inter individuels qui sont calculées une fois pour toutes.
4 La méthode de Ward (critère du moment centré
d'ordre 2)
Le moment centré d'ordre deux est équivalent à une
pondération de la distance entre centres de gravités. Ce
critère donne en générale les meilleures classifications.
Il est préférable de ne l'utiliser qu'avec des variables
métriques pour lesquelles la notion de moment est bien définie.
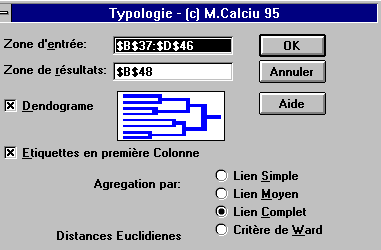
La zone d'entrée doit contenir un tableau ayant sur les lignes
les individus (observations) et en colonnes les valeurs des variables qui
caractérisent chaque individu.
Si l'option Etiquettes en première Colonne est cochée
la première colonne du tableau d'entrée est utilisée
comme étiquettes pour les individus et les variables.
La zone de résultats affiche un tableau exprimant le processus
de regroupements successifs. Chaque regroupement est caractérisé
par cinq éléments l'indicatif du Noeud symbolisant le regroupement
en cours les deux derniers noeuds et/ou observations (Gauche et Droit)
qu'il réunit, le Poids (le nombre total d'observations qui composent
le Noeud) et le Niveaux du Noeud dans la hiérarchie.
A partir de ce tableau on peut optionellement demander l'affichage
du dendogramme qui visualise cette hiérarchie.
La géo-typologie rajoute des contraintes de contiguïté
aux algorithmes de classification hiérarchique ascendante (voir
Typologie). A chaque itération sont fusionnés les groupes
qui se ressemblent le plus tout en étant contigus (au sens géographique
du terme).
Dans une zone d'entrée supplémentaire formé de deux
colonnes, appelée zone des contiguïtés sont marqués
les paires d'observations contigus.
Tous les autres paramètres sont les même que celles de l'option
Typologie.
L'analyse discriminante est une technique particulièrement adapté
aux études de segmentation des marchés. Elle exprime la relation
entre un ensemble de variables prédictives (similaire à celles
utilisées en régression) et l'appartenance à un groupe
(utilisateurs permanents et occasionnels d'un produit; acheteurs d'une
marque et les acheteurs de marques concurrentes; clients loyaux et aloyaux;
vendeurs bons, médiocres et mauvais).
Les tris croisés ou les tests de différences sont les vois
les plus utilisés pour explorer (voir décrire) la relation
entre l'appartenance à un groupe et autre variables catégorielles
(sexe, classe sociales etc.) ou numériques (revenu).
L'analyse discriminante a des buts plus ambitieux elle utilise les variables
prédictives pour expliquer et prédire le groupe auquel appartient
un individu.
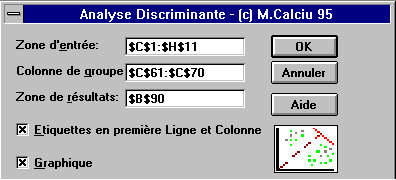
La zone des données doit contenir un tableau ayant sur les
lignes les individus (observations) et en colonnes les valeurs des variables
que caractérisent chaque individu.
La zone des groupes est une colonne (ou une ligne) ayant un nombre
de cellule égal au nombre d'individus. Elle contient les numéros
des groupes auxquels appartiennent les individus.
Si l'option Etiquettes en première Ligne est cochée
la première ligne du tableau des données est utilisée
comme étiquettes pour les variables.
L'option Graphiques cochée détermine l'affichage de
deux graphiques le premier représentant les coordonnées des
variables dans le plan des axes (fonctions) discriminants et le deuxième
les coordonnées des individus dans le même plan.
La zone de résultats commence dans la cellule indiquée
dans la boite de dialogue et contient deux tableaux rangés en colonnes.
Chaque colonne représente un axe (fonction) discriminant. Ces axes
forment un système de coordonnés orthogonales sur les quelles
on peut visualiser les variables et les observations.
Le premier tableau des facteurs discriminantes et des valeurs discriminantes.
1 dans la partie supérieure de la matrice rangés en
colonnes ce trouvent les coefficients des fonctions discriminantes qui
expriment les coefficients de pondération des variables dans la
combinaison linéaire qui forme chaque facteur discriminant. Ces
coefficients sont utiles pour calculer les scores des individus sur les
axes discriminantes choisies en fonction des quelles on détermine
l'appartenance des individus a un groupe.
2 sur la dernière ligne est calculé le pouvoir discriminant
de chaque axe a partir des valeurs propres, obtenues par des calculs qui
maximisent la variance intergroupe sous contrainte d'une variance intra
groupe unitaire.
Le deuxième tableau donne les coordonnées des individus
sur les axes discriminants. Il permet de vérifier la qualité
de la prédiction de l'appartenance à un groupe en comparant
les scores des individus sur un axe discriminant avec le score du centre
de gravité (de la moyenne) du groupe.
Ces fonctions matricielles ont comme arguments des matrices (qui ne doivent
contenir que des nombres) et retournent une matrice (voir au sujet des
fonctions matricielles les manuels et le système d'aide de Excel).
Pour pouvoir retourner une matrice, une zone de cellules qui accueillera
les résultats doit être présélectionnée
avant d'écrire ou modifier la fonction.
Vous pouvez les coller dans la zone sélectionnée, en utilisant
la commande Coller un fonction du Menu Sélections.
Voila une liste de ces fonctions:
Mat_x_Transp(matrice)
Renvoie le produit d'une matrice avec sa transposée
La zone présélectionnée pour la fonction doit avoir
le nombre de lignes et deux colonnes égale au nombre de lignes de
la matrice donnée en argument
Tranxp_x_Mat(matrice)
Renvoie le résultat de la premultiplication d'une matrice avec sa
transposée.
La zone présélectionnée pour la fonction doit avoir
le nombre de lignes et deux colonnes égale au nombre de colonnes
de la matrice donnée en argument
MatVarCov(matrice)
Renvoie la matrice des variances et covariances d'un tableau de données.
La zone présélectionnée pour la fonction doit avoir
le nombre de lignes et deux colonnes égale au nombre de colonnes
de la matrice donnée en argument
MatCorrel(matrice)
Renvoie la matrice des corrélations d'un tableau de données.
La zone présélectionnée pour la fonction doit avoir
le nombre de lignes et deux colonnes égale au nombre de colonnes
de la matrice donnée en argument
Vprop(matrice symétrique)
Renvoie les vecteurs et valeurs propres d'une matrice symétrique.
La zone présélectionnée pour la fonction doit avoir
une ligne et une colonne de plus par rapport à la matrice donnée
en argument (voir la rubrique Vecteurs et Valeurs propres pour plus de
détails).
AnaFact(matrice; "métrique normée (Oui/Non)?")
Renvoie les vecteurs et valeurs propres de la matrice variance covariance
(si la métrique n'est pas normée) ou de la matrice des corrélation
(si la métrique choisie est normée) calculées a partir
de la matrice donnée en argument.
La zone présélectionnée pour la fonction doit avoir
une ligne et une colonne de plus par rapport au nombre de colonnes matrice
donnée en argument (voir la rubrique Positionnement pour plus de
détails). Sur la dernière colonne sont affichées les
variances des variables.
AfCoresp(matrice)
Renvoie les vecteurs et valeurs propres de l'équivalent d'une matrice
variance covariance calculée à partir du tableau de contingence
donné en argument.
La zone présélectionnée pour la fonction doit avoir
une ligne de plus par rapport au nombre de colonnes du tableau donnée
en argument (voir la rubrique Analyse Factorielle des Correspondances pour
plus de détails).
AnaDisc(tableau numérique; colonne groupe)
Renvoie les coefficients discriminants et pouvoirs discriminants permettant
à expliquer l'appartenance des individus caractérisés
par les donnés du tableau numérique aux groupes indiqués
dans la colonne (ou ligne) des groupes .
La zone présélectionnée pour la fonction doit avoir
une ligne de plus par rapport au nombre de colonnes du tableau numérique
donné en argument (voir la rubrique Scoring pour plus de détails).
FactScores(matrice1; matrice2 (VectProp); "métrique normée
(Oui/Non)?")
Renvoie les scores des individus sur les axes factorielles en utilisant
comme arguments le tableau des données caractérisant les
individus sur plusieurs variables, la matrice des vecteurs propres et le
type de métrique utilisé dans le calcul de vecteurs propres.
La zone présélectionnée pour la fonction doit avoir
un nombre de lignes et deux colonnes égale au nombre de lignes et
colonnes que la première matrice donnée en argument
Typo("méthode S/C/A/W"; matrice)
Renvoie un tableau exprimant le processus de regroupements successifs qui
décrit la classification hiérarchique. La matrice donnée
en argument contient les données caractérisant les individus
sur plusieurs variables.
La zone présélectionnée pour la fonction doit
avoir cinq colonnes et une ligne de moins par rapport à la matrice
d'entrée (donnée en argument) (voir la rubrique Typologie
pour plus de détails).
TypoGeo("méthode S/A/C/W"; données; contiguïtés)
Renvoie un tableau exprimant le processus de regroupements successifs qui
décrit la classification hiérarchique sous contrainte de
contiguïté. La matrice donnée en argument contient les
données caractérisant les individus sur plusieurs variables.
La matrice des contiguïtés contient sur deux colonnes les paires
d'individus contigus.
La zone présélectionnée pour la fonction doit avoir
cinq colonnes et une ligne de moins par rapport à la matrice d'entrée
(donnée en argument) (voir les rubriques Typologie et Geo Typologie
pour plus de détails).
Dendograme(tableau de classification)
Renvoie un tableau qui permet d'illustrer graphiquement (par un graphique
de type XY en Excel) le dendogramme d'une classification hiérarchique.
La matrice donnée en argument est le tableau qui décrit le
processus de classification (voir ci-dessus et la rubrique Typologie pour
plus de détails) elle doit avoir cinq colonnes.
La zone présélectionnée pour la fonction doit avoir
trois colonnes. Le nombre de lignes est quatre fois le nombre majoré
de un des lignes de la matrice d'entrée (donnée en argument).
Un dendogramme graphique est obtenu en sélectionnant les dernières
deux colonnes du tableau renvoyé et en suivant la procédure
de création de graphiques de type XY de Excel.
NumClust(tableau de classification; no. groupes)
Renvoie l'appartenance des observations au groupes à un niveau spécifié
de la hiérarchie de classification. Ce niveau est fixé par
l'argument "no. groupes" qui exprime tout simplement le nombre
de groupes qu'on veut retenir. Le tableau résulté à
sur la première colonne le numéro de l'observation et sur
la deuxième colonne le numéro du groupe auquel elle appartient.
Le tableau donnée en argument est celui qui décrit le processus
de classification (voir ci-dessus et la rubrique Typologie pour plus de
détails). Il doit avoir cinq colonnes.
La zone présélectionnée pour la fonction doit avoir
deux colonnes. Le nombre de lignes est le nombre majoré de un des
lignes de la matrice d'entrée (donnée en argument).
Etapes a suivre:
A. pour installer le paquet MULTIVAR
1. Introduisez la disquette d'installation dans le lecteur a: et lancez
le programme d'installation en tapant:
a:install
Apres avoir lancé le programme d'installation (install.exe), vérifiez
éventuellement si les fichier évoqués ci-dessous (voir
rubrique fichiers et répertoires crées par le programme d'installation)
ont bien été copies et places dans les bons répertoires.
2. Lancez Excel sous Windows, sélectionnez dans le menu Options
la commande Macros complémentaires, appuyez sur le bouton Ajouter
et sélectionnez de la liste des fichiers et répertoires dans
le répertoire MULTIVAR le fichier multivar.xla et appuyez sur le
bouton OK.
3. Fermez le Gestionnaire de Macros Complémentaires. Quittez et
relancez Excel.
4. Maintenant le paquet Multivar est installe comme option permanente appelée
Analyse Multivariee dans le Menu Option de Excel 4 ou dans le Menu Outils
de Excel 5.
B. pour utiliser le paquet MULTIVAR après installation
1. Lancez Excel
2. Choisissez la commande Analyse Multivariee pour Excel4 dans le Menu
Options et pour Excel5 dans le Menu Outils.
Remarque: les fonctions matricielles d'analyse multivariée deviennent
disponibles et sont affichées dans la liste des fonctions de la
commande Coller un Fonction du Menu Sélection seulement après
avoir lancé une fois la commande Analyse Multivariée.
C. pour retirer l'option Analyse Multivariée du Menu
1. Sélectionnez dans le menu Options (Excel 4) ou Outils (Excel
5) la commande Macros complémentaires, sélectionnez la macro
Analyse Multivariée et appuyez sur le bouton retirer.
2. Fermez le Gestionnaire de Macros Complémentaires.
D. pour rajouter de manière permanente les fonctions d'analyse multivariée
à Excel
1. Sélectionnez dans le menu Options de Excel 4 (Outils pour Excel
5) la commande Macros
complémentaires, appuyez sur le bouton Ajouter et sélectionnez
de la liste des fichiers et répertoires dans le répertoire
C:\EXCEL\MACROLIB\MULTIVAR le fichier multivfn.xla et appuyez sur le bouton
OK.
2. Fermez le Gestionnaire de Macros Complémentaires
3. Maintenant les fonctions spéciales d'analyse multivariée
sont installées de manière permanente et peuvent être
intégrées dans vos calculs.
E. pour retirer les fonctions matricielles d'analyse multivariée
de Excel
1. Sélectionnez dans le menu Options (Excel 4) ou Outils (Excel
5) la commande Macros complémentaires, sélectionnez la macro
Fonctions Multivariée et appuyez sur le bouton Retirer.
2. Fermez le Gestionnaire de Macros Complémentaires.
Le programme d'installation doit:
- Créer le répertoire: C:\EXCEL\MACROLIB\MULTIVAR
- Copier dans C:\EXCEL\MACROLIB\MULTIVAR les fichiers:
macro complémentaires (.XLA):
- MULTIVAR.XLA
- VPROP.XLA
- ACP.XLA
- AFC.XLA
- TYPO.XLA
- ADISCR.XLA
et le fichier DLL (dynamic link libraries):
- MULTIVAR.DLL
- Copier le fichier MULTIVFN.XLA dans le répertoire C:\EXCEL\MACROLIB\MULTIVAR
- Copier le fichier d'aide MULTIVAR.HLP dans le répertoire C:\EXCEL.




